题目内容
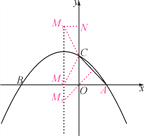
【题目】如图,已知抛物线y=-![]() x2-
x2-![]() x+2与x轴交于A,B两点,与y轴交于点C.
x+2与x轴交于A,B两点,与y轴交于点C.
(1)求点A,B,C的坐标;
(2)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

【答案】(1) 点A的坐标为(2,0),点B的坐标为(-4,0),点C的坐标为(0,2);(2) 点M坐标为(-1,-1)或(-1,2+![]() )或(-1,2-
)或(-1,2-![]() ).
).
【解析】试题分析:(1)由抛物线y=-![]() x2-
x2-![]() x+2与x轴交于A,B两点,与y轴交于点C,分别令y=0与x=0,即可求得答案;
x+2与x轴交于A,B两点,与y轴交于点C,分别令y=0与x=0,即可求得答案;
(2)分别从M,C,A为顶点去分析求解即可求得答案.
试题解析:(1)令y=0,得-![]() x2-
x2-![]() x+2=0,
x+2=0,
∴x2+2x-8=0,解得x1=-4,x2=2,
∴点A的坐标为(2,0),点B的坐标为(-4,0),
令x=0,得y=2,
∴点C的坐标为(0,2);
(2)①当C为等腰三角形的顶角的顶点时,CM1=CA=2![]() ,CM2=CA,
,CM2=CA,
作M1N⊥OC于N,则M1N=1.
在Rt△CM1N中,CN=![]() =
=![]() ,
,
∴点M1坐标为(-1,2+![]() ),点M2坐标为(-1,2-
),点M2坐标为(-1,2-![]() );
);
②当M3为等腰三角形的顶角的顶点时,
易求直线AC的表达式为y=-x+2,
∴线段AC的垂直平分线为y=x与对称轴的交点为M3(-1,-1),
∴点M3的坐标为(-1,-1);
③当点A为等腰三角形的顶角的顶点的三角形不存在,
综上所述:点M坐标为(-1,-1)或(-1,2+![]() )或(-1,2-
)或(-1,2-![]() ).
).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目