Question

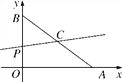
【题目】如图，在平面直角坐标系中，已知点A(4，0)和点B(0，3)，点C是AB的中点，点P在折线AOB上，直线CP截△AOB，所得的三角形与△AOB相似，那么点P的坐标是__________．

Answer 1

【答案】或(2，0)或(，0)

【解析】试题解析：当PC∥OA时，△BPC∽△BOA，由点C是AB的中点，所以P为OB的中点，此时P点坐标为（0， ）；
当PC∥OB时，△ACP∽△ABO，由点C是AB的中点，所以P为OA的中点，此时P点坐标为（2，0）；
当PC⊥AB时，如图，

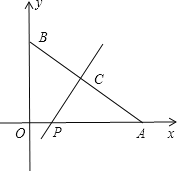
∵∠CAP=∠OAB，
∴Rt△APC∽Rt△ABC，

∴

∵点A（4，0）和点B（0，3），
∴AB==5，
∵点C是AB的中点，
∴AC=，
∴，
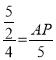∴AP=，
∴OP=OA-AP=4-=，
此时P点坐标为（，0），
综上所述，满足条件的P点坐标为（0， ），（2，0），（，0）．