Question

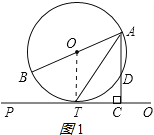
【题目】如图，AB为⊙O的直径，D、T是圆上的两点，且AT平分∠BAD，过点T作AD的延长线的垂线PQ，垂足为C．

（1）求证：PQ是⊙O的切线；

（2）已知⊙O的半径为2，若过点O作OE⊥AD，垂足为E，OE=，求弦AD的长．

Answer 1

【答案】（1）见解析；（2）AD=2

【解析】

试题分析：连接OT，根据OA=OT得出∠OAT=∠OTA，根据AT为角平分线得出∠OAT=∠CAT，从而得出OT∥AC，根据PQ⊥AC得出切线；根据垂径定理得出答案．

试题解析：（1）证明：连接OT，如图1所示： ∵OA=OT， ∴∠OAT=∠OTA， ∵AT平分∠BAD，

∴∠OAT=∠CAT， ∴∠OTA=∠CAT， ∴OT∥AC， ∵PQ⊥AC， ∴PQ⊥OT， ∴PQ是⊙O的切线；

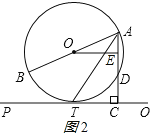
（2）解：如图2所示： ∵OE⊥AD， ∴AE=DE，∠AEO=90°，

∴AE===1， ∴AD=2AE=2．