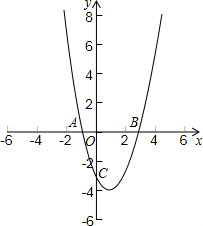题目内容
已知抛物线y=
x2+1(如图所示).
(1)填空:抛物线的顶点坐标是(______,______),对称轴是______;
(2)已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点N,使四边形OAMN为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.

| 1 |
| 4 |
(1)填空:抛物线的顶点坐标是(______,______),对称轴是______;
(2)已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点N,使四边形OAMN为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.

(1)顶点坐标是(0,1),对称轴是y轴(或x=O).
(2)∵△PAB是等边三角形,
∴∠ABO=90°-60°=30°.
∴AB=20A=4.
∴PB=4.
解法一:把y=4代入y=
x2+1,
得x=±2
.
∴P1(2
,4),P2(-2
,4).
解法二:∴OB=
=2
∴P1(2
,4).
根据抛物线的对称性,得P2(-2
,4).
(3)∵点A的坐标为(0,2),点P的坐标为(2
,4)
∴设线段AP所在直线的解析式为y=kx+b
∴
解得:
∴解析式为:y=
x+2
设存在点N使得OAMN是菱形,
∵点M在直线AP上,
∴设点M的坐标为:(m,
m+2)
如图,作MQ⊥y轴于点Q,则MQ=m,AQ=OQ-OA=
m+2-2=
m
∵四边形OAMN为菱形,
∴AM=AO=2,
∴在直角三角形AMQ中,AQ2+MQ2=AM2,
即:m2+(
m)2=22
解得:m=±
代入直线AP的解析式求得y=3或1,
当P点在抛物线的右支上时,分为两种情况:
当N在右图1位置时,
∵OA=MN,
∴MN=2,
又∵M点坐标为(
,3),
∴N点坐标为(
,1),即N1坐标为(
,1).
当N在右图2位置时,
∵MN=OA=2,M点坐标为(-
,1),
∴N点坐标为(-
,-1),即N2坐标为(-
,-1).
当P点在抛物线的左支上时,分为两种情况:
第一种是当点M在线段PA上时(PA内部)我们求出N点坐标为(-
,1);
第二种是当M点在PA的延长线上时(在第一象限)我们求出N点坐标为(
,-1)
∴存在N1(
,1),N2(-
,-1)N3(-
,1),N4(
,-1)使得四边形OAMN是菱形.

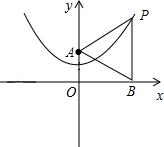
(2)∵△PAB是等边三角形,
∴∠ABO=90°-60°=30°.
∴AB=20A=4.
∴PB=4.
解法一:把y=4代入y=
| 1 |
| 4 |
得x=±2
| 3 |
∴P1(2
| 3 |
| 3 |
解法二:∴OB=
| AB2-OA2 |
| 3 |
∴P1(2
| 3 |
根据抛物线的对称性,得P2(-2
| 3 |
(3)∵点A的坐标为(0,2),点P的坐标为(2
| 3 |
∴设线段AP所在直线的解析式为y=kx+b
∴
|
解得:
|
∴解析式为:y=
| ||
| 3 |
设存在点N使得OAMN是菱形,
∵点M在直线AP上,
∴设点M的坐标为:(m,
| ||
| 3 |

如图,作MQ⊥y轴于点Q,则MQ=m,AQ=OQ-OA=
| ||
| 3 |
| ||
| 3 |
∵四边形OAMN为菱形,
∴AM=AO=2,
∴在直角三角形AMQ中,AQ2+MQ2=AM2,
即:m2+(
| ||
| 3 |
解得:m=±
| 3 |
代入直线AP的解析式求得y=3或1,
当P点在抛物线的右支上时,分为两种情况:
当N在右图1位置时,
∵OA=MN,
∴MN=2,
又∵M点坐标为(
| 3 |

∴N点坐标为(
| 3 |
| 3 |
当N在右图2位置时,
∵MN=OA=2,M点坐标为(-
| 3 |
∴N点坐标为(-
| 3 |
| 3 |
当P点在抛物线的左支上时,分为两种情况:
第一种是当点M在线段PA上时(PA内部)我们求出N点坐标为(-
| 3 |
第二种是当M点在PA的延长线上时(在第一象限)我们求出N点坐标为(
| 3 |
∴存在N1(
| 3 |
| 3 |
| 3 |
| 3 |



练习册系列答案
相关题目
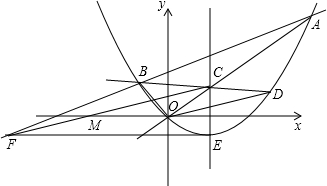

 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.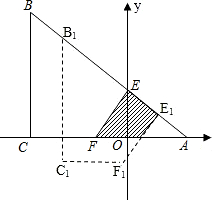 单位长度,平移中四边形BCFE与△AEF重叠的面积为S.
单位长度,平移中四边形BCFE与△AEF重叠的面积为S.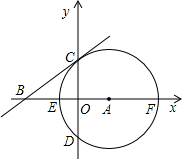 D两点,过C点作⊙A的切线BC交x轴于B.
D两点,过C点作⊙A的切线BC交x轴于B.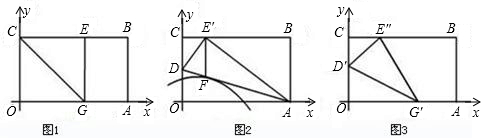
 ,与x轴相交于点F.
,与x轴相交于点F.