题目内容
如图,在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C,点C的坐标为(0,-3),且BO=CO.
(1)求出B点坐标和这个二次函数的解析式;
(2)求出y随x的增大而减小的自变量x的取值范围.
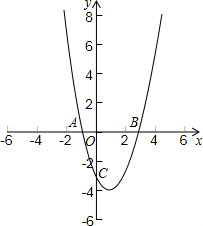
(1)求出B点坐标和这个二次函数的解析式;
(2)求出y随x的增大而减小的自变量x的取值范围.
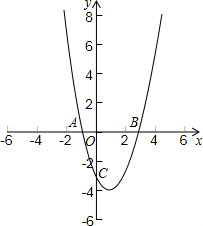
(1)∵点C的坐标为(0,-3),且BO=CO,
∴点B的坐标为(3,0),
把(0,-3),(3,0)代入y=ax2+bx+c得:9+3b+c=0,c=-3,
∴a=1,b=-2,
∴y=x2-2x-3;
(2)x=-
=-
=1,
由图象可得:当x<1时,y随x的增大而减小.
∴点B的坐标为(3,0),
把(0,-3),(3,0)代入y=ax2+bx+c得:9+3b+c=0,c=-3,
∴a=1,b=-2,
∴y=x2-2x-3;
(2)x=-
| b |
| 2a |
| -2 |
| 2 |
由图象可得:当x<1时,y随x的增大而减小.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.
正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.