��Ŀ����
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4cm������P��A��������������εı�����A��B��C��D�˶������˶���ʱ��Ϊt��s������APD�����ΪS��cm2����S��t�ĺ���ͼ����ͼ��ʾ����ش��������⣺
��1����P��AB���˶�ʱ��Ϊ�� ��s����CD���˶����ٶ�Ϊ�� ��cm/s����APD�����S�����ֵΪ�� ��cm2��
��2����S��t֮��ĺ�����ϵʽ��������S��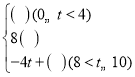 ��
��
��3��������˶�ʱ��tΪ����ʱ����APD�����Ϊ6cm2��
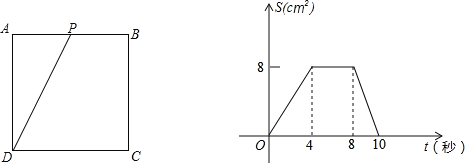
���𰸡���1��4��2��8����2��2t��4��t��8��40����3����tΪ3���![]() ��ʱ����APD�����Ϊ6cm2
��ʱ����APD�����Ϊ6cm2
��������
��1���۲�ͼ�ɵô𰸣�
��2��������ʱ��Σ��ֱ�����APD�������
��3������P��BC���˶�ʱ��S��Ϊ8����ˣ���APD�����Ϊ6ʱ��P��AB��CD�ϣ�������������ۣ�
�⣺��1���ɺ���ͼ���֪��P��AB���˶���ʱ��Ϊ4s����CD���˶���ʱ��Ϊ2s��
��CD��4cm��
��P��CD�ϵ��˶��ٶ�Ϊ4��2��2cm/s��
P��BC���˶�ʱ����APD��������Ϊ8cm2��
��2����0��t��4ʱ��P��AB���˶���
�ɺ���ͼ���֪��P��AB�ϵ��˶��ٶ�Ϊ4��4��1cm/s��
��AP��t��
��S��![]() ADAP��2t��
ADAP��2t��
��4��t��8ʱ��P��BC���˶���
��APD�����Ϊ��ֵ8����S��8��
��8��t��10ʱ��P��CD���˶���
DP��4��2��t��8������2t+20��
S��![]() ADDP����4t+40��
ADDP����4t+40��
����������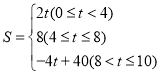 ��
��
��3����P��AB��ʱ��
��2t��6�����t��3s��
��P��CD��ʱ��
�4t+40��6�����t��![]() ��
��
������������tΪ3���![]() ��ʱ����APD�����Ϊ6cm2��
��ʱ����APD�����Ϊ6cm2��

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�