题目内容
【题目】如图,直线AC上取点B,在其同一侧作两个等边三角形△ABD 和△BCE ,连接AE,CD与GF,下列结论正确的有( )

① AE DC;②AHC120;③△AGB≌△DFB;④BH平分AHC;⑤GF∥AC
A.①②④B.①③⑤C.①③④⑤D.①②③④⑤
【答案】D
【解析】
根据等边三角形的性质得到BA=BD,BE=BC,∠ABD=∠CBE=60°,则可根据”SAS“判定△ABE≌△DBC,所以AE=DC,于是可对①进行判断;根据全等三角形的性质得到∠BAE=∠BDC,则可得到∠BAH+∠BCH=60°,从而根据三角形内角和得到∠AHC=120°,则可对②进行判断;利用”ASA”可证明△AGB≌△DFB,从而可对③进行判断;利用△ABE≌△DBC得到AE和DC边上的高相等,则根据角平分线的性质定理逆定理可对④进行判断;证明△BGF为等边三角形得到∠BGF=60°,则∠ABG=∠BGF,所以GF∥AC,从而可对⑤进行判断.
解:∵△ABD和△BCE都是等边三角形,
∴BA=BD,BE=BC,∠ABD=∠CBE=60°,
∵∠DBE=180°60°60°=60°,
∴∠ABE=∠DBC=120°,
∵BA=BD,∠ABD=∠DBC,BE=BC,
∴△ABE≌△DBC(SAS),
∴AE=DC,所以①正确;
∠BAE=∠BDC,
∵∠BDC+∠BCD=∠ABD=60°,
∴∠BAE+∠BCD=60°,
∴∠AHC=180°(∠BAH+∠BCH)=180°60°=120°,所以②正确;
∵∠BAG=∠BDF,BA=BD,∠ABG=∠DBF=60°,
∴△AGB≌△DFB(ASA);所以③正确;
∵△ABE≌△DBC,
∴AE和DC边上的高相等,
即B点到AE和DC的距离相等,
∴BH平分∠AHC,所以④正确;
∵△AGB≌△DFB,
∴BG=BF,
∵∠GBF=60°,
∴△BGF为等边三角形,
∴∠BGF=60°,
∴∠ABG=∠BGF,
∴GF∥AC,所以⑤正确.
故选D.

 阅读快车系列答案
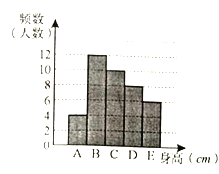
阅读快车系列答案【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行调查,已知抽取的样本中,男生和女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
|
|
|
|
|
|
|
|
|
|
男生身高情况直方图
女生身高情况扇形统计图
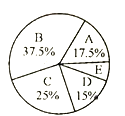
根据图表提供的信息,回答下列问题:
(1)求样本中男生的人数.
(2)求样本中女生身高在E组的人数.
(3)已知该校共有男生380人,女生320人,请估计全校身高在![]() 之间的学生总人数.
之间的学生总人数.




