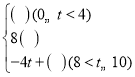题目内容
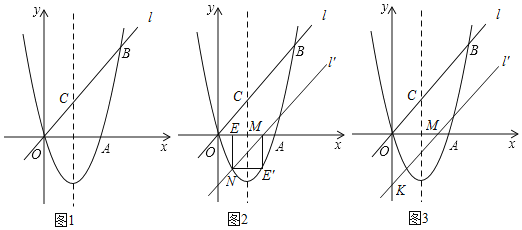
【题目】如图1,经过原点O的抛物线y=ax2+bx(a、b为常数,a≠0)与x轴相交于另一点A(3,0).直线l:y=x在第一象限内和此抛物线相交于点B(5,t),与抛物线的对称轴相交于点C.
(1)求抛物线的解析式;
(2)在x轴上找一点P,使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似,求满足条件的点P的坐标;
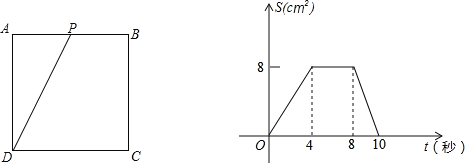
(3)直线l沿着x轴向右平移得到直线l′,l′与线段OA相交于点M,与x轴下方的抛物线相交于点N,过点N作NE⊥x轴于点E.把△MEN沿直线l′折叠,当点E恰好落在抛物线上时(图2),求直线l′的解析式;
(4)在(3)问的条件下(图3),直线l′与y轴相交于点K,把△MOK绕点O顺时针旋转90°得到△M′OK′,点F为直线l′上的动点.当△M'FK′为等腰三角形时,求满足条件的点F的坐标.
【答案】(1)抛物线的解析式为:y=![]() ;(2)点P坐标为(5,0)或(
;(2)点P坐标为(5,0)或(![]() ,0)(3)y=x﹣2;(4)F坐标为(1,0)或(﹣1,﹣2).
,0)(3)y=x﹣2;(4)F坐标为(1,0)或(﹣1,﹣2).
【解析】(1)应用待定系数法进行求解即可得;
(2)分两种情况△OBA∽△OCP、△OBA∽△OPC分别讨论进行求解即可;
(3)由已知直线l′与x轴所夹锐角为45°,△EMN为等腰直角三角形,当沿直线l′折叠时,四边形ENE′M为正方形,表示点N、E′坐标带入抛物线解析式,可解;
(4)由(3)图形旋转可知,M′K′⊥直线l′,△M'FK′只能为等腰直角三角形,则分类讨论可求解.
(1)由已知点B坐标为(5,5)
把点B(5,5),A(3,0)代入y=ax2+bx,得
![]() ,解得:
,解得: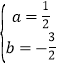 ,
,
∴抛物线的解析式为:y=![]() ;
;
(2)由(1)抛物线对称轴为直线x=![]() ,则点C坐标为(
,则点C坐标为(![]() ,
,![]() ),
),
∴OC=![]() ,OB=5
,OB=5![]() ,
,
当△OBA∽△OCP时,![]() ,∴
,∴![]() ,∴OP=
,∴OP=![]() ,
,
当△OBA∽△OPC时,![]() ,∴
,∴![]() ,∴OP=5,
,∴OP=5,
∴点P坐标为(5,0)或(![]() ,0);
,0);
(3)设点N坐标为(a,b),直线l′解析式为:y=x+c,
∵直线l′y=x+c与x轴夹角为45°,
∴△MEN为等腰直角三角形,
当把△MEN沿直线l′折叠时,四边形ENE′M为正方形,
∴点′E坐标为(a﹣b,b),
∵EE′平行于x轴,
∴E、E′关于抛物线对称轴对称,
∵![]() ,
,
∴b=2a﹣3,
则点N坐标可化为(a,2a﹣3),
把点N坐标代入y=![]() 得:2a﹣3=
得:2a﹣3=![]() ,
,
解得:a1=1,a2=6,
∵a=6时,b=2a﹣3=﹣9<0,
∴a=6舍去,
则点N坐标为(1,﹣1),
把N坐标带入y=x+c,则c=﹣2,
∴直线l′的解析式为:y=x﹣2;
(4)由(3)K点坐标为(0,﹣2),
则△MOK为等腰直角三角形,
∴△M′OK′为等腰直角三角形,M′K′⊥直线l′,
∴当M′K′=M′F时,△M'FK′为等腰直角三角形,
∴F坐标为(1,0)或(﹣1,﹣2).

 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案【题目】某班对道德与法治,历史,地理三门程的选考情况进行调研,数据如下:
科目 | 道德与法治 | 历史 | 地理 |
选考人数(人) | 19 | 13 | 18 |
其中道德与法治,历史两门课程都选了的有3人,历史,地理两门课程都选了的有4人,该班至多有多少学生( )
A.41B.42C.43D.44