题目内容
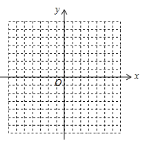
【题目】如图,在平面直角坐标系![]() 中,双曲线
中,双曲线![]() =
=![]() 经过□
经过□![]() 的顶点
的顶点![]() 、
、![]() ,点
,点![]() 的坐标为(
的坐标为(![]() ,
,![]() 1),点
1),点![]() 在
在![]() 轴上,且
轴上,且![]() ∥
∥![]() 轴,平行四边形
轴,平行四边形![]() 的面积是8.
的面积是8.
(1)求双曲线和AB所在直线的解析式;
(2)点![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )是双曲线
)是双曲线![]() =
=![]() (
(![]() <0)图象上的两点,若
<0)图象上的两点,若![]() >
>![]() ,则
,则![]()
![]() ;(填“<”、“=”或“>”)
;(填“<”、“=”或“>”)

【答案】(1)![]() ,y=6x-1;(2)<.
,y=6x-1;(2)<.
【解析】
(1)D点直接代入反比例函数即可得到反比例函数解析式,由平行四边形性质可得到A、B两点坐标,然后代入一次函数解析式,即可解得一次函数解析式 (2)利用反比例函数性质可直接得到结果
(1)D点坐标为(-2,-1)直接代入反比例函数解析式,得到k=2,即反比例函数解析式为![]() ;因为
;因为![]() ∥
∥![]() 轴,所以A点坐标为(0,-1),又因为平行四边形的面积为8,AD=2,所以平行四边形的高为4,得到B点纵坐标为3,B点又在反比例函数上,代入函数得到x=
轴,所以A点坐标为(0,-1),又因为平行四边形的面积为8,AD=2,所以平行四边形的高为4,得到B点纵坐标为3,B点又在反比例函数上,代入函数得到x=![]() ,所以B点坐标为(
,所以B点坐标为(![]() ,3);设直线AB的函数解析式为y=kx+b,将A(0,-1),B(
,3);设直线AB的函数解析式为y=kx+b,将A(0,-1),B(![]() ,3)代入一次函数解析式得到方程0=-k+b,3=
,3)代入一次函数解析式得到方程0=-k+b,3=![]() k+b,解两个方程得到k=6,b=-1,所以一次函数解析式为y=6x-1
k+b,解两个方程得到k=6,b=-1,所以一次函数解析式为y=6x-1
故双曲线解析式为![]() ,直线AB的解析式为y=6x-1
,直线AB的解析式为y=6x-1
(2)利用反比例函数性质,当k>0,x<0时,y随x增大而减小,因为![]() >
>![]() ,所以
,所以![]() <
<![]()

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】某学校计划组织全校1500名师生外出参加集体活动.经过研究,决定租用当地租车公司一共60辆![]() 、
、![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 400元 |
| 20人 | 300元 |
注:载客量指的是每辆客车最多可载该校师生的人数.
学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过22000元,一共有几种租车方案?并结合函数性质说明哪种租车方案最省钱?