ЬтФПФкШн
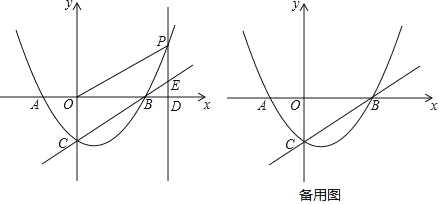
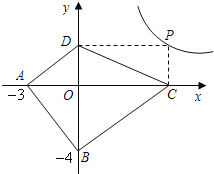
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌжБЯпABЗжБ№гыxжсЁЂyжсНЛгкBЁЂAСНЕуЃЌOAЁЂOBЕФГЄЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љ12x+32=0ЕФСНИіЪЕЪ§ИљЃЌЧвOBЃОOAЃЌвдOAЮЊвЛБпзїШчЭМЫљЪОЕФе§ЗНаЮAOCDЃЌCDНЛABгкЕуPЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
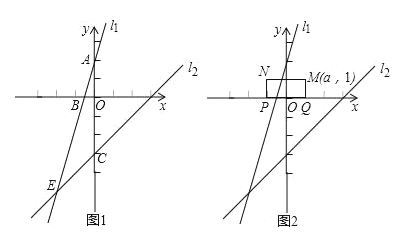
ЃЈ2ЃЉдкxжсЩЯЪЧЗёДцдквЛЕуQЃЌЪЙвдPЁЂCЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїADPЯрЫЦЃПШєДцдкЃЌЧѓЕуQзјБъЃЛЗёдђЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩшNЪЧЦНУцФквЛЖЏЕуЃЌдкyжсЩЯЪЧЗёДцдкЕуMЃЌЪЙЕУвдAЁЂCЁЂMЁЂNЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛЗёдђЃЌЧыЫЕУїРэгЩЃЎ
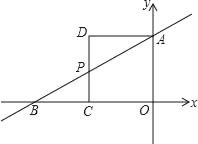
ЁОД№АИЁПЃЈ1ЃЉy=![]() x+4ЃЛЃЈ2ЃЉДцдкТњзуЬѕМўЕФЕуQЃЌЦфзјБъЮЊЃЈЉ8ЃЌ0ЃЉЛђЃЈ0ЃЌ0ЃЉЛђЃЈЉ3ЃЌ0ЃЉЛђЃЈЉ5ЃЌ0ЃЉЃЛЃЈ3ЃЉДцдкТњзуЬѕМўЕФMЕуЃЌЦфзјБъЮЊЃЈ0ЃЌ4+4
x+4ЃЛЃЈ2ЃЉДцдкТњзуЬѕМўЕФЕуQЃЌЦфзјБъЮЊЃЈЉ8ЃЌ0ЃЉЛђЃЈ0ЃЌ0ЃЉЛђЃЈЉ3ЃЌ0ЃЉЛђЃЈЉ5ЃЌ0ЃЉЃЛЃЈ3ЃЉДцдкТњзуЬѕМўЕФMЕуЃЌЦфзјБъЮЊЃЈ0ЃЌ4+4![]() ЃЉЛђЃЈ0ЃЌ4Љ4
ЃЉЛђЃЈ0ЃЌ4Љ4![]() ЃЉЛђЃЈ0ЃЌ0ЃЉЃЎ
ЃЉЛђЃЈ0ЃЌ0ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЗНГЬПЩЧѓЕУOAЁЂOBЕФГЄЃЌдђПЩЧѓЕУ![]() ЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУжБЯп
ЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшQ(x,0)ЃЌдђCQ=|x+4|ЃЌЗж![]() КЭ
КЭ![]() СНжжЧщПіЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЗжБ№ЕУЕНЙигк
СНжжЧщПіЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЗжБ№ЕУЕНЙигк![]() ЕФЗНГЬЃЌдђПЩЧѓЕУ
ЕФЗНГЬЃЌдђПЩЧѓЕУ![]() ЕФжЕЃЌПЩЧѓЕУ
ЕФжЕЃЌПЩЧѓЕУ![]() ЕузјБъЃЛ
ЕузјБъЃЛ
ЃЈ3ЃЉЕБ![]() ЮЊСтаЮЕФБпЪБЃЌдђга
ЮЊСтаЮЕФБпЪБЃЌдђга![]() ПЩЧѓЕУ
ПЩЧѓЕУ![]() ЕузјБъЃЛЕБ
ЕузјБъЃЛЕБ![]() ЮЊЖдНЧЯпЪБЃЌгЩЭМаЮПЩжЊ
ЮЊЖдНЧЯпЪБЃЌгЩЭМаЮПЩжЊ![]() ЕуМДЮЊЫљЧѓЃЌПЩЧѓЕУ
ЕуМДЮЊЫљЧѓЃЌПЩЧѓЕУ![]() ЕузјБъЃЎ
ЕузјБъЃЎ
ЪдЬтНтЮіЃК(1)НтЗНГЬ![]() ПЩЕУx=4Лђx=8ЃЌ
ПЩЕУx=4Лђx=8ЃЌ
ЁпOAЁЂOBЕФГЄЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬ![]() ЕФСНИіЪЕЪ§ИљЃЌЧвOB>OAЃЌ
ЕФСНИіЪЕЪ§ИљЃЌЧвOB>OAЃЌ
ЁрOA=4ЃЌOB=8ЃЌ
ЁрA(0,4),B(8,0)ЃЌ
ЩшжБЯпABНтЮіЪНЮЊy=kx+bЃЌ
Ёр![]() НтЕУ
НтЕУ
ЁржБЯпABНтЮіЪНЮЊ![]()
(2)ЁпЫФБпаЮAOCDЮЊе§ЗНаЮЃЌ
ЁрAD=CD=OC=OA=4ЃЌ
ЁрC(4,0)ЃЌ
дк![]() жаЃЌСюx=4ЃЌПЩЕУy=2ЃЌ
жаЃЌСюx=4ЃЌПЩЕУy=2ЃЌ
ЁрPC=PD=2ЃЌ
ЩшQ(x,0)ЃЌдђCQ=|x+4|ЃЌ
ЁпвдPЁЂC.QЮЊЖЅЕуЕФШ§НЧаЮгыЁїADPЯрЫЦЃЌ
ЁргаЁїPCQЁзЁїPDAКЭЁїPCQЁзЁїADPСНжжЧщПіЃЌ
ЂйЕБЁїPCQЁзЁїPDAЪБ,дђга![]() ,МД
,МД![]() ,НтЕУx=0Лђx=8,ДЫЪБQЕузјБъЮЊ(8,0)Лђ(0,0)ЃЛ
,НтЕУx=0Лђx=8,ДЫЪБQЕузјБъЮЊ(8,0)Лђ(0,0)ЃЛ
ЂкЕБЁїPCQЁзЁїADPЪБ,дђга![]() МД
МД![]() ,НтЕУx=3Лђx=5,ДЫЪБQЕузјБъЮЊ(3,0)Лђ(5,0)ЃЛ
,НтЕУx=3Лђx=5,ДЫЪБQЕузјБъЮЊ(3,0)Лђ(5,0)ЃЛ
злЩЯПЩжЊДцдкТњзуЬѕМўЕФЕуQ,ЦфзјБъЮЊ(8,0)Лђ(0,0)Лђ(3,0)Лђ(5,0)ЃЛ
(3)гЩЬтвтПЩЩшM(0,y)ЃЌ
ЁпA(0,4),C(4,0)ЃЌ
Ёр![]()
ЕБACЮЊСтаЮЕФвЛБпЪБ,дђгаAC=AM,МД|y4|=![]() ,НтЕУy=4ЁР
,НтЕУy=4ЁР![]() ,ДЫЪБMЕузјБъЮЊ
,ДЫЪБMЕузјБъЮЊ![]() Лђ
Лђ![]()
ЕБACЮЊСтаЮЕФЖдНЧЯпЪБ,дђгаMA=MC,гЩЬтвтПЩжЊДЫЪБMЕуМДЮЊOЕу,ДЫЪБMЕузјБъЮЊ(0,0)ЃЛ
злЩЯПЩжЊДцдкТњзуЬѕМўЕФMЕу,ЦфзјБъЮЊ![]() Лђ
Лђ![]() Лђ(0,0).
Лђ(0,0).

 ЦпаЧЭМЪщПкЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
ЦпаЧЭМЪщПкЫуЫйЫуЬьЬьСЗЯЕСаД№АИ