��Ŀ����
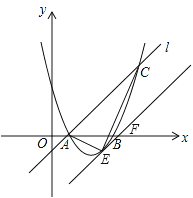
����Ŀ����ͼ����֪������y=ax2+bx+3��x�ύ��A��B���㣬����A��ֱ��l�������߽��ڵ�C������A��������ǣ�1��0����C�������ǣ�4��3����

��1���������ߵĽ���ʽ��
��2���ڣ�1���������ߵĶԳ������Ƿ���ڵ�D��ʹ��BCD���ܳ���С�������ڣ������D�����꣬�������ڣ���˵�����ɣ�
��3������E�ǣ�1�����������ϵ�һ�����㣬��λ��ֱ��AC���·���������ACE����������E������꣮
���𰸡��⣺��1����������y=ax2+bx+3������A��1��0������C��4��3����
��![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪy=x2��4x+3��
��2�����ڡ�
����A��B���ڶԳ���Գƣ�����DΪAC��Գ���Ľ���ʱ��BCD���ܳ���С��
��y=x2��4x+3=��x��2��2��1���������ߵĶԳ���Ϊֱ��x=2��
��ֱ��AC�Ľ���ʽΪy=kx+b��k��0����
��![]() ����ã�
����ã�![]() ��
��
��ֱ��AC�Ľ���ʽΪy=x��1��
��x=2ʱ��y=2��1=1��
�������߶Գ����ϴ��ڵ�D��2��1����ʹ��BCD���ܳ���С��
��3����ͼ�������E��ֱ��ACƽ���ߵ�ֱ��Ϊy=x+m��
����![]() ������y�ã�x2��5x+3��m=0��
������y�ã�x2��5x+3��m=0��
����=����5��2��4��1����3��m��=0��m=![]() ��
��
��m=![]() ʱ����E��AC�ľ��������ACE��������
ʱ����E��AC�ľ��������ACE��������
��ʱx=![]() ��y=
��y=![]() ��
��
����E��������![]() ��
��![]() ����
����
�����E��ֱ����x�ύ��ΪF����F��![]() ��0����
��0����
��AF=![]() ��
��
��ֱ��AC�Ľ���ʽΪy=x��1�����CAB=45����
����F��AC�ľ���Ϊ![]() ��
��
����![]() ��
��
���ACE��������![]() ����ʱE������Ϊ��
����ʱE������Ϊ��![]() ��
��![]() ����
����
��������
���⣨1�����ô���ϵ��������κ�������ʽ��ɡ�
��2�����ô���ϵ�������ֱ��AC�Ľ���ʽ��Ȼ�������Գ�ȷ�����·�����⣬ֱ��AC��Գ���Ľ��㼴Ϊ�����D��
��3������ֱ��AC�Ľ���ʽ���������E��ACƽ�е�ֱ�ߣ�Ȼ���������߽���ʽ��������y�õ�����x��һԪ���η��̣����ø����б�ʽ��=0ʱ����ACE��������Ȼ�������ʱ��ACƽ�е�ֱ�ߣ�Ȼ�������E�����꣬�������ֱ����x��Ľ���F�����꣬�����AF���ٸ���ֱ��l��x��ļн�Ϊ45�������ֱ��ľ��룬�����AC��ľ��룬Ȼ�����������ε������ʽ��ʽ���㼴�ɵý⡣

 �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д� �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�




