题目内容
【题目】如图，已知抛物线y＝
x2－4x＋7与y＝
x交于A、B两点(点A在点B左侧)．
(1)求A、B两点坐标；
(2)求抛物线顶点C的坐标，并求△ABC面积．
【答案】(1)A(2，1)，B(7， 
)；（2）
.
【解析】试题分析：（1）求曲线的交点，只需要联立方程组.
(2)利用顶点坐标公式求顶点，过C作x轴平行线，可以 得到△BCD，△ACD同底不等高，因为（1）已经求出A,B点坐标，所以可以得到△BCD，△ACD的高，最后求出两个三角形面积，作差就可以得到△ABC面积.
试题解析：解：(1)联立
,
解得
或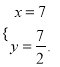
∴A(2，1)，B(7， 
)．
(2)∵y＝
x2－4x＋7＝
(x－4)2－1，
∴顶点坐标为C(4，－1)．
过C作CD∥x轴交直线AB于D.
∵y＝
x，
令y＝－1，得
x＝－1，解得x＝－2.
∴D(－2，－1)．∴CD＝6.
∴S△ABC＝S△BCD－S△ACD
＝
×6×(
＋1)－
×6×(1＋1)
＝
.
练习册系列答案
相关题目
