题目内容
【题目】已知：如图，在菱形ABCD中， BE⊥AD于点E，延长AD至F，使DF=AE，连接CF．
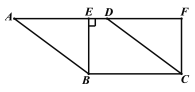
（1）判断四边形EBCF的形状，并证明；
（2）若AF=9，CF=3，求CD的长．
【答案】（1）四边形EBCF是矩形，证明见解析；（2）CD =5
【解析】
（1）由菱形的性质证得EF=BC，由此证明四边形EBCF是平行四边形.，再利用BE⊥AD即可证得四边形EBCF是矩形；
（2）设CD=x，根据菱形的性质及矩形的性质得到DF=9-x，再利用勾股定理求出答案.
（1）四边形EBCF是矩形
证明：∵四边形ABCD菱形，
∴AD=BC，AD∥BC.
又∵DF=AE，
∴DF+DE=AE+DE，
即：EF = AD.
∴ EF = BC.
∴四边形EBCF是平行四边形.
又∵BE⊥AD，
∴ ∠BEF=90°.
∴四边形EBCF是矩形.
（2） ∵ 四边形ABCD菱形，
∴ AD=CD.
∵ 四边形EBCF是矩形，
∴ ∠F=90°.
∵AF=9，CF=3，
∴设CD=x， 则DF=9-x，
∴ 
，
解得：
∴CD =5.
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
