题目内容
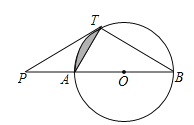
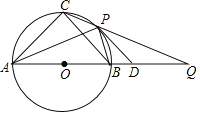
【题目】如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为![]() 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论:①若∠PAB=30°,则
上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论:①若∠PAB=30°,则![]() 的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6
的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6![]() ;④无论点P在
;④无论点P在![]() 上的位置如何变化,CPCQ为定值.其中正确的是________________.(写出所有正确结论的序号)
上的位置如何变化,CPCQ为定值.其中正确的是________________.(写出所有正确结论的序号)
【答案】②③④
【解析】
①根据∠POB=60°,OB=6,即可求得弧![]() 的长;②根据切线的性质以及垂径定理,即可得到
的长;②根据切线的性质以及垂径定理,即可得到![]() ,据此可得AP平分∠CAB;③根据BP=BO=PO=6,可得△BOP是等边三角形,据此即可得出PD=6
,据此可得AP平分∠CAB;③根据BP=BO=PO=6,可得△BOP是等边三角形,据此即可得出PD=6![]() ;④判定△ACP∽△QCA,即可得到
;④判定△ACP∽△QCA,即可得到![]() ,即CPCQ=CA2,据此可得CPCQ为定值.
,即CPCQ=CA2,据此可得CPCQ为定值.
如图,连接OP,
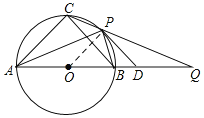
∵AO=OP,∠PAB=30°,
∴∠POB=60°,
∵AB=12,
∴OB=6,
∴弧![]() 的长为
的长为![]() =2π,故①错误;
=2π,故①错误;
∵PD是⊙O的切线,
∴OP⊥PD,
∵PD∥BC,
∴OP⊥BC,
∴![]() ,
,
∴∠PAC=∠PAB,
∴AP平分∠CAB,故②正确;
若PB=BD,则∠BPD=∠BDP,
∵OP⊥PD,
∴∠BPD+∠BPO=∠BDP+∠BOP,
∴∠BOP=∠BPO,
∴BP=BO=PO=6,即△BOP是等边三角形,
∴PD=![]() OP=6
OP=6![]() ,故③正确;
,故③正确;
∵AC=BC,
∴∠BAC=∠ABC,
又∵∠ABC=∠APC,
∴∠APC=∠BAC,
又∵∠ACP=∠QCA,
∴△ACP∽△QCA,
∴![]() ,即CPCQ=CA2(定值),故④正确;
,即CPCQ=CA2(定值),故④正确;
故答案为:②③④.

【题目】今年五一期间采石矶景区将启用新的大门,景区决定利用现有的不同种类花卉设计出两种不同的造型A和B摆放于大门广场.已知每个A种造型的成本y1与造型个数x(0<x<60)满足关系式y1=82﹣![]() x,每个B种造型的成本y2与造型个数x(0<x<60)的关系如表所示:
x,每个B种造型的成本y2与造型个数x(0<x<60)的关系如表所示:
x(个) | … | 10 | 20 | 30 | 50 | … |
y2(元) | … | 93 | 86 | 79 | 65 | … |
(1)请求出y2与x的函数关系式;
(2)现在广场需搭配A、B两种园艺造型共60个,要求每种园艺造型不得少于20个,并且成本总额W(元)不超过5000元.以上要求能否同时满足?请你通过计算说明理由.
【题目】在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
试验种子n(粒) | 1 | 5 | 50 | 100 | 200 | 500 | 1000 | 2000 | 3000 |
发芽频数m | 1 | 4 | 45 | 92 | 188 | 476 | 951 | 1900 | 2850 |
发芽频率 | 0 | 0.80 | 0.90 | 0.92 | 0.94 | 0.952 | 0.951 | a | b |
(1)计算表中a,b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100kg麦种,则有多少千克的麦种可以成活为秧苗?