Question

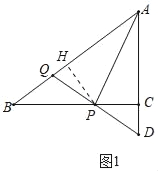
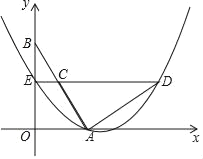
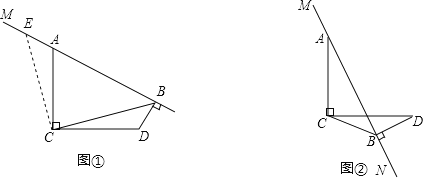
【题目】如图1，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，动点P在线段BC上，点Q在线段AB上，且PQ＝BQ，延长QP交射线AC于点D．

（1）求证：QA＝QD；

（2）设∠BAP＝α，当2tanα是正整数时，求PC的长；

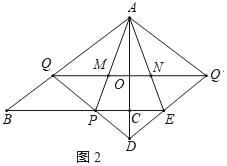
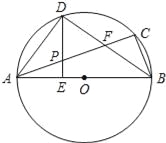
（3）作点Q关于AC的对称点Q′，连结QQ′，AQ′，DQ′，延长BC交线段DQ′于点E，连结AE，QQ′分别与AP，AE交于点M，N（如图2所示）．若存在常数k，满足kMN＝PEQQ′，求k的值．

Answer 1

【答案】（1）证明见解析（2）PC的长为或（3）8

【解析】

（1）由等腰三角形的性质得出∠B＝∠BPQ＝∠CPD，由直角三角形的性质得出∠BAC＝∠D，即可得出结论；

（2）过点P作PH⊥AB于H，设PH＝3x，BH＝4x，BP＝5x，由题意知tanα＝1或，当tanα＝1时，HA＝PH＝3x，与勾股定理得出3x+4x＝5，解得x＝，即可求出PC长；

当tanα＝时，HA＝2PH﹣6x，得出6x+4x＝5，解得x＝，即可求出PC长；

（3）设QQ′与AD交于点O，由轴对称的性质得出AQ′＝AQ＝DQ＝DQ′，得出四边形AQDQ′是菱形，由菱形的性质得出QQ′⊥AD，AO＝AD，证出四边形BEQ'Q是平行四边形，得出QQ′＝BE，设CD＝3m，则PC＝4m，AD＝3+3m，即QQ′﹣BE＝4m+4，PE＝8m，由三角函数得出＝tan∠PAC＝，即可得出结果．

（1）证明：∵PQ＝BQ，

∴∠B＝∠BPQ＝∠CPD，

∵∠ACB＝∠PCD＝90°，

∴∠A+∠BAC＝90°，∠D+∠CPD＝90°，

∴∠BAC＝∠D，

∴QA＝QD；

（2）解：过点P作PH⊥AB于H，如图1所示：

设PH＝3x，BH＝4x，BP＝5x，

由题意得：tan∠BAC＝，∠BAP＜∠BAC，

∴2tanα是正整数时，tanα＝1或，

当tanα＝1时，HA＝PH＝3x，

∴3x+4x＝＝5，

∴x＝，

即PC＝4﹣5x＝；

当tanα＝时，HA＝2PH﹣6x，

∴6x+4x＝5，

∴x＝，

即PC＝4﹣5x＝；

综上所述，PC的长为或；

（3）解：设QQ′与AD交于点O，如图2所示：

由轴对称的性质得：AQ′＝AQ＝DQ＝DQ′，

∴四边形AQDQ′是菱形，

∴QQ′⊥AD，AO＝AD，

∵BC⊥AC，

∴QQ′∥BE，

∵BQ∥EQ′，

∴四边形BEQ'Q是平行四边形，

∴QQ′＝BE，

设CD＝3m，则PC＝4m，AD＝3+3m，

即QQ′﹣BE＝4m+4，PE＝8m，

∵＝tan∠PAC＝，

∴＝，

即MN＝2MO＝4m（1+m），

∴k＝＝＝8．