题目内容
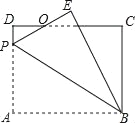
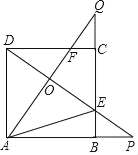
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中,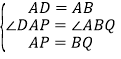 ,
,
∴△DAP≌△ABQ,
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP;
故①正确;
∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴![]() ,
,
∴AO2=ODOP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OEOP;故②错误;
在△CQF与△BPE中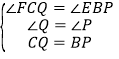 ,
,
∴△CQF≌△BPE,
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,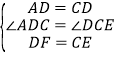 ,
,
∴△ADF≌△DCE,
∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,
即S△AOD=S四边形OECF;故③正确;
∵BP=1,AB=3,
∴AP=4,
∵△AOP∽△DAP,
∴![]() ,
,
∴BE=![]() ,∴QE=
,∴QE=![]() ,
,
∵△QOE∽△PAD,
∴![]() ,
,
∴QO=![]() ,OE=
,OE=![]() ,
,
∴AO=5﹣QO=![]() ,
,
∴tan∠OAE=![]() =
=![]() ,故④正确,
,故④正确,
故选C.

练习册系列答案
相关题目