题目内容
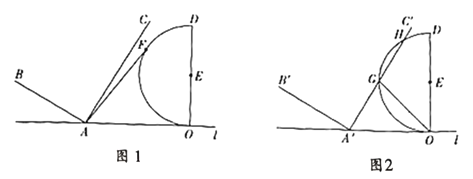
【题目】如图,某处有一座信号塔AB,山坡BC的坡度为1:![]() ,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
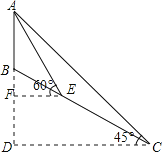
(1)求出山坡BC的坡角∠BCD的大小;
(2)求塔顶A到CD的铅直高度AD.(结果保留整数:![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)
【答案】∠BCD=30°;(2)塔顶A到CD的铅直高度AD约为137米.
【解析】
(1)根据tan∠BCD=![]() ,进而得出答案;
,进而得出答案;
(2)设AD=x,则CD=AD=x,可得AF=x-50,EF=x-50![]() ,进而利用在Rt△AEF中,
,进而利用在Rt△AEF中,![]() =tan60°,求出答案.
=tan60°,求出答案.
(1)依题意得:tan∠BCD=![]() =
=![]() ,
,
∴∠BCD=30°;
(2)作EG⊥CD,垂足为G.

在Rt△CEG中,CE=100,∠ECG=30°,
∴EG=CEsin30°=50,
CG=CEcos30°=50![]() ,
,
设AD=x,则CD=AD=x.
∴AF=x-50,EF=x-50![]() ,
,
在Rt△AEF中,![]() =tan60°,
=tan60°,
∴![]() .
.
解得:x=50![]() +50≈136.5(米).
+50≈136.5(米).
答:塔顶A到CD的铅直高度AD约为137米.

练习册系列答案
相关题目