题目内容
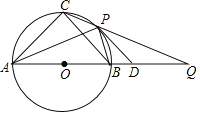
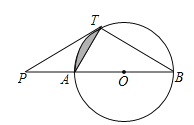
【题目】如图,直线![]() 与
与![]() 相切于点T,直线
相切于点T,直线![]() 与
与![]() 相交于
相交于![]() 两点,连接
两点,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,请直接写出图中阴影部分的面积(结果保留无理数)
,请直接写出图中阴影部分的面积(结果保留无理数)
【答案】(1)见解析;(2)![]()
【解析】
(1)利用切线的性质得∠OTP=90°,即∠2+∠PTA=90°,再利用圆周角定理得到∠ATB=90°,则∠2+∠1=90°,然后利用等量代换得到∠PTA=∠B;
(2)利用TP=TB得到∠P=∠B,而∠POT=2∠B,所以∠POT=2∠P,则利用∠OTP=90°可计算出∠P=30°,∠POT=60°,利用含30度的直角三角形三边的关系得到OT=6,△AOT为等边三角形,然后根据扇形的面积公式和图中阴影部分的面积=S扇形AOT-S△AOT进行计算.
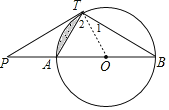
(1)证明:∵直线PT与⊙O相切于点T,
∴OT⊥PT,
∴∠OTP=90°,
即∠2+∠PTA=90°,
∵AB为直径,
∴∠ATB=90°,
∴∠2+∠1=90°,
∴∠PTA=∠1,
∵OB=OT,
∴∠1=∠B,
∴∠PTA=∠B;
(2)解:∵PT=BT,
∴∠P=∠B,
∵∠POT=∠B+∠1=2∠B,
∴∠POT=2∠P,
而∠OTP=90°,
∴∠P=30°,∠POT=60°,
∴OT=![]() PT=6,△AOT为等边三角形,
PT=6,△AOT为等边三角形,
∴图中阴影部分的面积=S扇形AOT-S△AOT=![]() -
-![]() =6π-9
=6π-9![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目