��Ŀ����
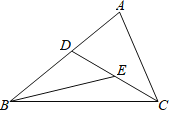
����Ŀ������ABC�У���A��90����AB��4��AC��3��M��AB�ϵĶ��㣨����A��B�غϣ�����M����MN��BC��AC�ڵ�N����MNΪֱ������O�����ڡ�O�����ڽӾ���AMPN����AM��x��

��1����ͼ1���ú�x�Ĵ���ʽ��ʾ����NP�����S��
��2����ͼ2����O��ֱ��BC����D�㣬��x��ֵΪ���٣�
��3���ڶ���M���˶������У�������NP������BCNM�غϵ����Ϊy������y����x�ĺ�������ʽ������xΪ��ֵʱ��y��ֵ������ֵ�Ƕ��٣�
���𰸡���1��s=![]() ��0��x��4������2��x=
��0��x��4������2��x=![]() ����3����x=
����3����x=![]() ʱ,yֵ������ֵ��2��
ʱ,yֵ������ֵ��2��
��������
��1����ƽ���á�AMN�ס�ABC���������������ζ�Ӧ�߶γɱ������ú�x�Ĵ���ʽ��ʾ��AN��MN����Ͼ��ε����ʿ������MNP�������
��2������OD����M����MQ��BC���������Ӧ�Ƿֱ���ȵ��������������ƿɵá�BQM�ס�BAC�������������ζ�Ӧ�߶γɱ����ɵ�x��ֵ��
��3��M�����˶��Ĺ����У�P������BC�ϣ�����AP��O�����AP���е㣬�ɡ�AMO�ס�ABP���Ƶ����ʿɵ�AM=2��������������ۢٵ�0��x��2ʱ���غϲ��ֵ������Ϊ��MNP��������ɣ�1���ɵ�y����x�ĺ�������ʽ������x��ȡֵ��Χȷ��y���ֵ���ɣ��ڵ�2��x��4ʱ����PM��BC��E��PN��BC��F�����þ���AMPN��ƽ���ı���MBFN�����ʿ��ú�x��ʽ�ӱ�ʾ��PF���ɡ�PEF�ס�ABC�����ʿɵ�![]() ������������غϲ��ֵ����
������������غϲ��ֵ����![]() �ɵ�y����x�ĺ�������ʽ����Ϻ�������ʽ���Ա���x��ȡֵ��Χ�ɵ�y�����ֵ.
�ɵ�y����x�ĺ�������ʽ����Ϻ�������ʽ���Ա���x��ȡֵ��Χ�ɵ�y�����ֵ.
��1����������ABC��A=900��AB=4��AC=3
��BC=5
��MN//BC
���AMN�ס�ABC
��![]()
��![]()
��AN=![]() ��MN=
��MN=![]()
�֡�AMPNΪ����
����PM=AN=![]() ��PN=AM=x
��PN=AM=x
���ԡ�MNP�����s=PM��PN��![]() =
=![]()
��s=![]() ��0��x��4��
��0��x��4��
��2��AM=x,��MB=4-x
��ͼ������OD��DΪ�е㣬��M����MQ��BC��QΪ���㣻
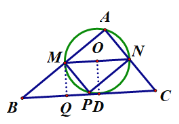
������ɵã�OD=OM=ON=![]()
��MN��BC
��OD��BC��MQ��BC
��MQ=OD=![]()
�ߡ�A=��MQB=900����B=��B
���BQM�ס�BAC
��![]()
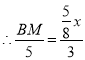
��BM=![]()
![]()
��x=![]()
���Ե�x=![]() ʱ����O��ֱ��BC����D��.
ʱ����O��ֱ��BC����D��.
��3��M�����˶��Ĺ����У�P������BC�ϣ���ͼ

����AP��O�����AP���е�.
��MN��BC
���AMO�ס�ABP
��![]()
��AM=2
�ʷ�����������ۣ�
�ٵ�0��x��2ʱ
��MNP������BCNM�غϵ����![]()
![]()
��x=2ʱ��y�����ֵy=![]()
�ڵ�2��x��4ʱ����ͼ
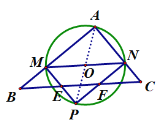
��PM��BC��E��PN��BC��F
AM=x����MB=4-x
���ı���AMPN�Ǿ��Σ�
��PN��AM��PN=AM=x
�֡�MN��BC
���ı���MBFN��ƽ���ı���
![]()
![]()
�֡ߡ�PEF�ס�ABC
��![]()
S��PEF=![]()
![]()
![]()
![]() =
=![]()
�൱x=![]() ʱ������2��x��4��y�����ֵ��y=2
ʱ������2��x��4��y�����ֵ��y=2
������������x=![]() ��yֵ������ֵ��2��
��yֵ������ֵ��2��

 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�