题目内容
已知点G是△ABC的重心，GP∥BC交AC边于点P，如果BC=12，那么GP=分析：根据GP∥BC，即可证得：△AGP∽△ADC，然后根据重心的性质，求得
=
，然后根据相似三角形的对应边的比相等即可求解．
| AG |
| AD |
| 2 |
| 3 |
解答：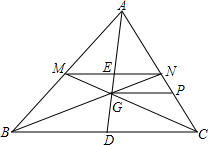
解：∵G是△ABC的重心，
∴
=2，
∴
=
．
∵GP∥BC，
∴△AGP∽△ADC，
∴
=
=
，
又∵CD=
BC=6，
∴GP=4．
故答案是：4．
解：∵G是△ABC的重心，∴
| AG |
| DG |
∴
| AG |
| AD |
| 2 |
| 3 |
∵GP∥BC，
∴△AGP∽△ADC，
∴
| GP |
| CD |
| AG |
| AD |
| 2 |
| 3 |
又∵CD=
| 1 |
| 2 |
∴GP=4．
故答案是：4．
点评：本题主要考查了相似三角形的性质，以及三角形的重心的性质，正确求得
=
是解题关键．
| AG |
| AD |
| 2 |
| 3 |
练习册系列答案
相关题目
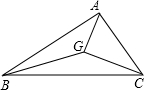如图，已知点G是△ABC的重心，AG=5，GC=12，AC=13，则BG=
18、如图，已知点D是△ABC的边BC（不含点B，C）上的一点，DE∥AB交AC于点E，DF∥AC交AB于点F、要使四边形AFDE是矩形，则在△ABC中要增加的一个条件是：