题目内容
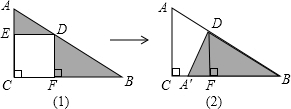
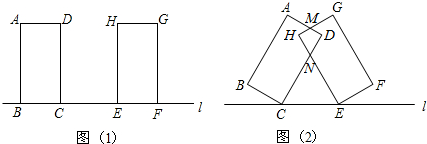
已知，DE是等腰直角三角形ABC的中位线，将△BED沿AB翻折使E落在F处，如图①，再将△ABC绕B点逆时针旋转α°（0＜α＜90°），连接AF，DC，如图②．
（1）观察猜想，∠AFB与∠BDC大小关系______（直接出正确结论）；
（2）当α=30时，试判断△BDC的形状；
（3）在（2）的条件下，若DG=1，求DF的长．
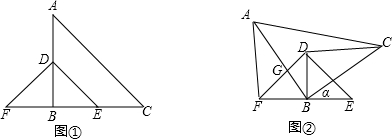
（1）观察猜想，∠AFB与∠BDC大小关系______（直接出正确结论）；
（2）当α=30时，试判断△BDC的形状；
（3）在（2）的条件下，若DG=1，求DF的长．
（1）∵DE是等腰直角三角形ABC的中位线，将△BED沿AB翻折使E落在F处，
∴∠EDB=∠A=∠FDB=45°，∠DBE=∠DBF=90°，FD=DE，
∴FB=BE=BD，
∠CBD+∠ABD=90°，∠ABD+∠ABF=90°，
∴∠CBD=∠ABF，
在△CBD和△ABF中
∵
，
∴△CBD≌△ABF（SAS），
∴∠AFB=∠BDC．
故答案为：∠AFB=∠BDC；
（2）如图②，延长BD至M使DM=BD，连接MC，则BM=2DB，
∵DE是等腰直角三角形ABC的中位线，
∴△BDE是等腰直角三角形，
∵BM=BC，BC=2BD，BC=2CE，BE=BD，
∴BC=BM，
∵∠CBE=30°，
∴∠DBC=60°，
∴△BMC为等边三角形，
∴DC⊥BD，
∴△DCB直角三角形；
（3）设DB=a，∴BC=2a，
∴DC=
=
a，
∴AF=
a，
∵∠AFB=∠BDC，
∴∠AFB=90°，
∴AF∥DB，
∴
=
=
=
，
∵DG=1，
∴FG=
，
∴DF=
+1．
∴∠EDB=∠A=∠FDB=45°，∠DBE=∠DBF=90°，FD=DE，
∴FB=BE=BD，
∠CBD+∠ABD=90°，∠ABD+∠ABF=90°，
∴∠CBD=∠ABF，
在△CBD和△ABF中
∵
|
∴△CBD≌△ABF（SAS），
∴∠AFB=∠BDC．
故答案为：∠AFB=∠BDC；
（2）如图②，延长BD至M使DM=BD，连接MC，则BM=2DB，∵DE是等腰直角三角形ABC的中位线，
∴△BDE是等腰直角三角形，
∵BM=BC，BC=2BD，BC=2CE，BE=BD，
∴BC=BM，
∵∠CBE=30°，
∴∠DBC=60°，
∴△BMC为等边三角形，
∴DC⊥BD，
∴△DCB直角三角形；
（3）设DB=a，∴BC=2a，
∴DC=
| 4a2-a2 |
| 3 |
∴AF=
| 3 |
∵∠AFB=∠BDC，
∴∠AFB=90°，
∴AF∥DB，
∴
| DG |
| GF |
| DB |
| AF |
| a | ||
|
| ||
| 3 |
∵DG=1，
∴FG=
| 3 |
∴DF=
| 3 |
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
