��Ŀ����
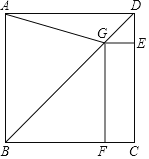
����Ŀ��������̽�� ̽��������ͼ1��ͼ3�У���ABC�����Ϊa ��
��1����ͼ1, �ӳ���ABC�ı�BC����D��ʹCD=BC������DA������ACD�����ΪS1����S1=________���ú�a�Ĵ���ʽ��ʾ����




��2����ͼ2���ӳ���ABC�ı�BC����D���ӳ���CA����E��ʹCD=BC��AE=CA������DE������DEC�����ΪS2����S2= ���ú�a�Ĵ���ʽ��ʾ����
��3����ͼ2�Ļ������ӳ�AB����F��ʹBF=AB������FD��FE���õ���DEF����ͼ3��������Ӱ���ֵ����ΪS3����S3=__________���ú�a�Ĵ���ʽ��ʾ����
���֣�����������������ABC���߾�˳���ӳ�һ�����������ö˵㣬�õ���DEF����ͼ3������ʱ�����dz���ABC������չ��һ�Σ����Է��֣���չһ�κ�õ�����DEF�������ԭ����ABC�����_____����
���𰸡���1��a����2��2a����3��6a��7.
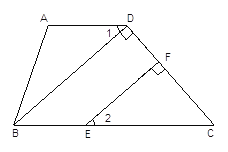
��������(1)���ݵȵȸߵ������������Ƚ��;(2)�ֱ��A��E��BD�Ĵ���,������������λ�߶����������ε������ʽ��⼴��;(3)�ɡ�BFD����ECD����AEF�ı߳�Ϊ��ABC�߳���һ��,�����AEF�ĸ���Ƚ��.
��:(1) ��CD=BC, ��ABC�����Ϊa, ��ABC���ACD�ĸ����,![]() ;
;
(2)�ֱ��A��E��AG��BD,EF��BD,G��FΪ����,
��AG��EF,��AΪCE���е�,![]() ,
,
��BC=CD,![]() ;
;
(3) �ߡ�BDF�ı߳�BD�ǡ�ABC�߳�BC��2��,�������ε�����Ϊ��һ���������ߵ��ӳ���,![]() ,�ߡ�ABC�����Ϊa,
,�ߡ�ABC�����Ϊa,![]() .ͬ���ɵ�,
.ͬ���ɵ�,![]() ,
,![]() ,
,![]() .
. ![]() ,
,![]() ,
,![]() ,
,
����չһ�κ�õ��ġ�DEF�������ԭ����ABC�����7��.

 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�����Ŀ��ij�̳�Ͷ��13 800Ԫ�ʽ��ס������ֿ�Ȫˮ��500�䣬��Ȫˮ�ijɱ��ۺ����ۼ������ʾ��
���/���� | �ɱ��� | ���ۼ�(Ԫ/��) |
�� | 24 | 36 |
�� | 33 | 48 |
(1)���̳������ס������ֿ�Ȫˮ�������䣿
(2)ȫ������500���Ȫˮ�����̳�������������Ԫ��