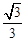题目内容
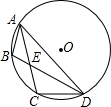
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P。
(1)求证:AP是⊙O的切线;
(2)若OC=CP,AB=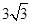 ,求CD的长。
,求CD的长。

(1)求证:AP是⊙O的切线;
(2)若OC=CP,AB=
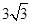 ,求CD的长。
,求CD的长。(1)证明见解析;(2)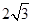 .
.
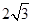 .
.试题分析:(1)连接AO,AC(如图).欲证AP是⊙O的切线,只需证明OA⊥AP即可;
(2)利用(1)中切线的性质在Rt△OAP中利用边角关系求得∠ACO=60°.然后在Rt△BAC、Rt△ACD中利用余弦三角函数的定义知AC=3,CD=
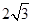 .
.试题解析:(1)证明:如图,连结AO,AC.

∵BC是⊙O的直径,
∴∠BAC=∠CAD=90°.
∵E是CD的中点,
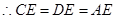 .
.∴∠ECA=∠EAC.
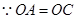 ,
,∴∠OAC=∠OCA.
∵CD是⊙O的切线,
∴CD⊥OC.
∴∠ECA+∠OCA=90°.
∴∠EAC+∠OAC=90°.
即∠OAP=90°
∴OA⊥AP.
∵A是⊙O上一点,
∴AP是⊙O的切线.
(2)解:由(1)知OA⊥AP.
在Rt△OAP中,∵∠OAP=90°,OC=CP=OA,即OP=2OA,
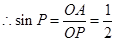 .
.∴∠P=30°.
∴∠AOP=60°.
∵OC=OA,
∴∠ACO=60°.
在Rt△BAC中,∵∠BAC=90°,AB=
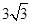 ,∠ACO=60°,
,∠ACO=60°, .
.又∵在Rt△ACD中,∠CAD=90°,∠ACD=90°-∠ACO=30°,
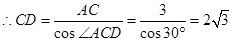 .
. 考点: 1.切线的判定与性质;2.解直角三角形.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
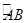 )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .
)对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .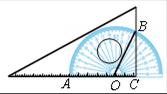
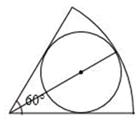
 ,
, ,则
,则 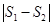 =_________(平方单位).
=_________(平方单位).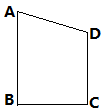
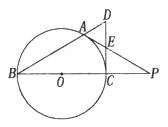
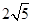 为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为
为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为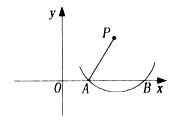
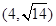
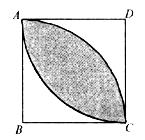
 )
)
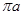 B.
B. 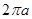 C.
C. 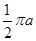 D.
D. 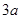
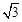 ,0)和点B(0,2), C是优弧
,0)和点B(0,2), C是优弧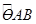 上的任意一点(不与点O,B重合),则tan∠BCO的值为( )
上的任意一点(不与点O,B重合),则tan∠BCO的值为( )