题目内容
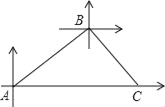
【题目】如图,在![]() 中,
中,![]() ,
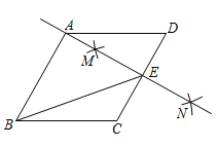
,![]() 是∠BAC的平分线,经过
是∠BAC的平分线,经过![]() 、
、![]() 两点的圆的圆心
两点的圆的圆心![]() 恰好落在
恰好落在![]() 上,
上,![]() 分别与
分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() .
.
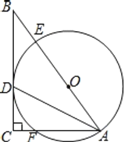
(1)判断直线![]() 与
与![]() 的位置关系并证明;
的位置关系并证明;
(2)若![]() 的半径为2,
的半径为2,![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)直线BC与⊙O相切,证明过程见解析;(2)![]() .
.
【解析】
(1)连接OD,根据角平分线的定义和等腰三角形的性质得出∠CAD=∠ODA,进而得出![]() ,根据平行线的性质即可得出∠ODB=∠C=90°,则可证明直线BC与⊙O相切;
,根据平行线的性质即可得出∠ODB=∠C=90°,则可证明直线BC与⊙O相切;
(2)首先根据![]() 可得出△BDO∽△BCA,进而有
可得出△BDO∽△BCA,进而有![]() ,从而求出BE的长度,然后利用勾股定理即可求出BD的长度.
,从而求出BE的长度,然后利用勾股定理即可求出BD的长度.
解:(1)直线BC与⊙O相切,证明如下:
证明:连接OD.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∵OD=OA,
∴∠OAD=∠ODA.
∴∠CAD=∠ODA.
∴OD∥AC.
∴∠ODB=∠C=90°,
即OD⊥BC.
又∵BC过半径OD的外端点D,
∴BC与⊙O相切.
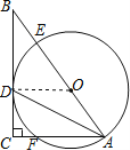
(2)由(1)知OD∥AC.
∴△BDO∽△BCA.
∴![]()
∵⊙O的半径为2,
∴DO=OE=2,AE=4.
∴![]() .
.
∴BE=2.
∴BO=4,
∴在Rt△BDO中,![]() .
.

练习册系列答案
相关题目
【题目】疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 | 5 | 10 | 20 | 50 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的众数和中位数分别是( )
A.100,10B.10,20C.17,10D.17,20