题目内容
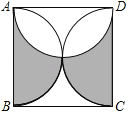
【题目】如图，正方形ABCD的边长为4，分别以正方形的三边为直径在正方形内部作半圆，则阴影部分的面积之和是（ ）
A.8B.4C.16πD.4π
【答案】A
【解析】
先判断出两半圆交点为正方形的中心，连接OA，OD，则可得出所产生的四个小弓形的面积相等，先得出2个小弓形的面积，即可求阴影部分面积．
解：由题意，易知两半圆的交点即为正方形的中心，设此点为O，连接AO，DO，
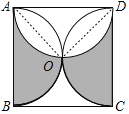
则图中的四个小弓形的面积相等，
∵两个小弓形面积＝S半圆AOD-S△AOD=S半圆AOD-
S正方形ABCD，
又正方形ABCD的边长为4，得各半圆的半径为2，
∴两个小弓形面积＝
×π×22﹣×4×4=2π﹣4，
∴S阴影＝2×S半圆﹣4个小弓形面积＝π22﹣2（2π﹣4）＝8，
故选：A．
练习册系列答案
相关题目
