题目内容
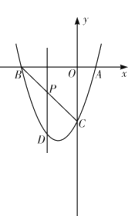
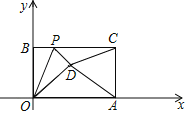
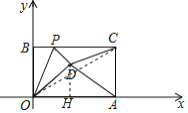
【题目】如图，已知一个矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（10，0），点B（0，6），点P为BC边上的动点，将△OBP沿OP折叠得到△OPD，连接CD、AD．则下列结论中：①当∠BOP＝45°时，四边形OBPD为正方形；②当∠BOP＝30°时，△OAD的面积为15；③当P在运动过程中，CD的最小值为2
﹣6；④当OD⊥AD时，BP＝2．其中结论正确的有（ ）
A.1个B.2个C.3个D.4个
【答案】D
【解析】
①由矩形的性质得到
，根据折叠的性质得到
，
，
，推出四边形
是矩形，根据正方形的判定定理即可得到四边形为正方形；故①正确；
②过
作
于
，得到
，
，根据直角三角形的性质得到
，根据三角形的面积公式得到
的面积为
，故②正确；
③连接
，于是得到
，即当
时，
取最小值，根据勾股定理得到的最小值为
；故③正确；
④根据已知条件推出
，，
三点共线，根据平行线的性质得到
，等量代换得到
，求得
，根据勾股定理得到
，故④正确．
解：①
四边形
是矩形，
，
将
沿
折叠得到
，
，，，
，
，
，
，
四边形是矩形，
，
四边形为正方形；故①正确；
②过作于，
点
，点
，
，，
，
，
，
，
的面积为，故②正确；
③连接，
则，
即当时，取最小值，
，，
，
，
即的最小值为；故③正确；
④
，
，
，
，
，，三点共线，
，
，
，
，
，
，
，
，故④正确；
故选：．
练习册系列答案
相关题目
