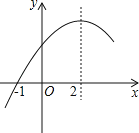ЬтФПФкШн
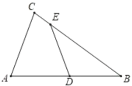
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁЯACB=90ЁуЃЌOC=2OBЃЌtanЁЯABC=2ЃЌЕуBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎХзЮяЯпy=Љx2+bx+cОЙ§AЁЂBСНЕуЃЎ
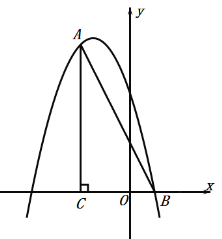
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧжБЯпABЩЯЗНХзЮяЯпЩЯЕФвЛЕуЃЌЙ§ЕуPзїPDДЙжБxжсгкЕуDЃЌНЛЯпЖЮABгкЕуEЃЌЪЙPEзюДѓЃЎ
ЂйЧѓЕуPЕФзјБъКЭPEЕФзюДѓжЕЃЎ
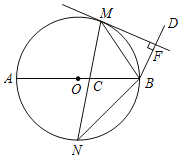
ЂкдкжБЯпPDЩЯЪЧЗёДцдкЕуMЃЌЪЙЕуMдквдABЮЊжБОЖЕФдВЩЯЃЛШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2Љ3x+4ЃЛЃЈ2ЃЉЂй![]() ЃЌP
ЃЌP![]() Ђк MЃЈ
Ђк MЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШИљОнвбжЊЧѓЕуAЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЂйИљОнAЃЈЉ2ЃЌ6ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌЧѓЕУABЕФНтЮіЪНЮЊЃКy=Љ2x+2ЃЌЩшPЃЈaЃЌЉa2Љ3a+4ЃЉЃЌдђEЃЈaЃЌЉ2a+2ЃЉЃЌРћгУPE=Љa2Љ3a+4Љ(Љ2a+2)=Љ(a+![]() )2+
)2+![]() ЃЌИљОнЖўДЮКЏЪ§ЕФЭМЯёгыаджЪМДЧѓНтЃЛ
ЃЌИљОнЖўДЮКЏЪ§ЕФЭМЯёгыаджЪМДЧѓНтЃЛ
ЂкИљОнЕуMдквдABЮЊжБОЖЕФдВЩЯЃЌЕУЕНЁЯAMB=90ЁуЃЌМДAM2+BM2=AB2![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌ
ЃЌ![]() ЃЌAB2ЙЪПЩСаГіЗНГЬЧѓНт.
ЃЌAB2ЙЪПЩСаГіЗНГЬЧѓНт.
НтЃКЃЈ1ЃЉЁпBЃЈ1ЃЌ0ЃЉ
ЁрOB=1ЃЌ
ЁпOC=2OB=2ЃЌ
ЁрBC=3 ,CЃЈЉ2ЃЌ0ЃЉ
RtЁїABCжаЃЌtanЁЯABC=2ЃЌ
Ёр![]() =2ЃЌ
=2ЃЌ
ЁрAC=6ЃЌ
ЁрAЃЈЉ2ЃЌ6ЃЉЃЌ
АбAЃЈЉ2ЃЌ6ЃЉКЭBЃЈ1ЃЌ0ЃЉДњШыy=Љx2+bx+cЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКy=Љx2Љ3x+4ЃЛ
ЃЈ2ЃЉЂйЁпAЃЈЉ2ЃЌ6ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌ
взЕУABЕФНтЮіЪНЮЊЃКy=Љ2x+2ЃЌ
ЩшPЃЈaЃЌЉa2Љ3a+4ЃЉЃЌдђEЃЈaЃЌЉ2a+2ЃЉЃЌ
ЁрPE=Љa2Љ3a+4Љ(Љ2a+2)=Љa2Љa+2=Љ(a+![]() )2+
)2+![]()
ЁрЕБa=![]() ЪБЃЌPE
ЪБЃЌPE![]() =
=![]() ,ДЫЪБP(
,ДЫЪБP(![]() ,
,![]() )
)
ЂкЁпMдкжБЯпPDЩЯЃЌЧвP(![]() ,
,![]() )ЃЌ
)ЃЌ
![]()
Ёр
![]() +
+![]()
AB2=32+62=45ЃЌ
ЁпЕуMдквдABЮЊжБОЖЕФдВЩЯ
ДЫЪБЁЯAMB=90ЁуЃЌ
ЁрAM2+BM2=AB2ЃЌ
Ёр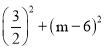 +
+![]() +
+![]() =45
=45
НтЕУЃК![]() ,
,![]()
ЁрMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ