题目内容
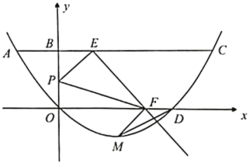
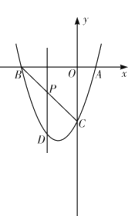
【题目】如图,在平面直角坐标系![]() 中,
中,![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 轴的负半轴上,
轴的负半轴上,![]() ,
,![]() 在反比例函数
在反比例函数![]() (
(![]() )的图象上,
)的图象上,![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,若
,若![]() 的面积是3,则
的面积是3,则![]() 的值是_________.
的值是_________.

【答案】![]()
【解析】
由题意,设点A(![]() ,0),B(0,
,0),B(0,![]() ),E(0,c),得到
),E(0,c),得到![]() ,过点D作DF⊥x轴,与x轴交于点F,过点C作CG⊥DF,与DF相交于点G,然后证明△ABO≌△CGD,△AEO∽△ADF,利用比例求出线段的长度,得到点C、D的坐标,代入反比例函数解析式,得到
,过点D作DF⊥x轴,与x轴交于点F,过点C作CG⊥DF,与DF相交于点G,然后证明△ABO≌△CGD,△AEO∽△ADF,利用比例求出线段的长度,得到点C、D的坐标,代入反比例函数解析式,得到![]() ,即可求出答案.
,即可求出答案.
解:由题意,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 轴的负半轴上,点E在y轴上,
轴的负半轴上,点E在y轴上,
设点A(![]() ,0),B(0,
,0),B(0,![]() ),E(0,c),
),E(0,c),
∴OA=![]() ,OB=b,OE=c,
,OB=b,OE=c,
∵![]() 的面积是3,
的面积是3,
∴![]() ,
,
∴![]() ;
;
过点D作DF⊥x轴,与x轴交于点F,过点C作CG⊥DF,与DF相交于点G,
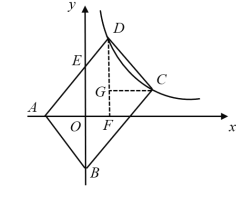
∴DF∥y轴,
∴![]() ,
,
∵AD∥BC,
∴![]() ,
,
∴![]() ,
,
∵∠ABC=∠CDA,
∴∠ABE=∠CDG,
∵∠AOB=∠CGD=90°,AB=CD,
∴△ABO≌△CGD,
∴DG=OB=b,CG=AO=a,
∵DF∥BE,
∴△AEO∽△ADF,
∴![]() ,
,
在Rt△AOE中,勾股定理得
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点C、D在![]() 的图像上,
的图像上,
∴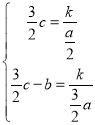 ,化简得:
,化简得:![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
故答案为:![]() .
.

练习册系列答案
相关题目