题目内容
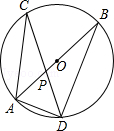
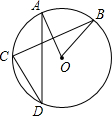
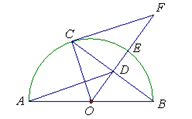
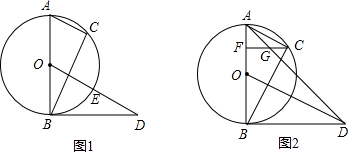
如图，AB是半圆O上的直径，E是的中点，OE交弦BC于点D，过点C作⊙O切线交OE的延长线于点F. 已知BC=8，DE=2.
(1)求⊙O的半径；
(2)求CF的长；
(3)求tan∠BAD 的值。
(1)求⊙O的半径；
(2)求CF的长；
(3)求tan∠BAD 的值。
解：⑴在⊙O中∵E是的中点 ∴OE⊥BC
∴BD＝
BC=×8="4."
在Rt△OBD中，设⊙O的半径为r．
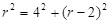
解得ｒ＝5.
(2) ∵CF是⊙O切线 ∴OC⊥CF
可以证明Rt△OCD∽Rt△OCE
∴
∴
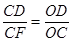
(3)过点D作DG⊥AB垂足为G
在Rt△ADG中
DG=
AG=AO＋OG=5＋
=
tan∠BAD =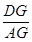
=
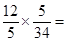
∴BD＝
BC=×8="4." 在Rt△OBD中，设⊙O的半径为r．
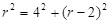
解得ｒ＝5.
(2) ∵CF是⊙O切线 ∴OC⊥CF
可以证明Rt△OCD∽Rt△OCE
∴
∴
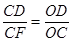
(3)过点D作DG⊥AB垂足为G
在Rt△ADG中
DG=
AG=AO＋OG=5＋= tan∠BAD =
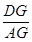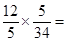
= （1）根据垂径定理可得△BOD为直角三角形，根据勾股定理求出半径；
（2）由1得OD=3，证明△COF∽△DOC，利用线段比求出CF；
（3）过点D作DM⊥AB于M，则可求DM、OM、AM的长，则tan∠BAD的值可求．
（2）由1得OD=3，证明△COF∽△DOC，利用线段比求出CF；
（3）过点D作DM⊥AB于M，则可求DM、OM、AM的长，则tan∠BAD的值可求．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
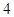，其中一个圆的半径长为
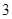，那么当两圆内切时，另一圆的半径为 ．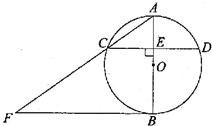
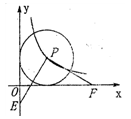
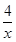上，以P为圆心的⊙P与两坐标轴都相切，E为y轴负半轴上的一点，PF⊥PE交x轴于点F，则OF－OE的值是 ___________．
