题目内容
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
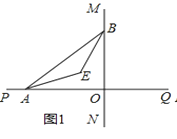
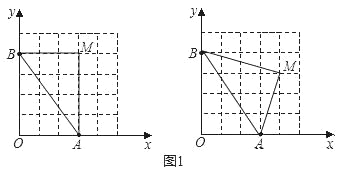
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标.
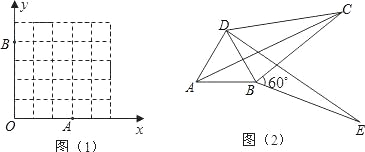
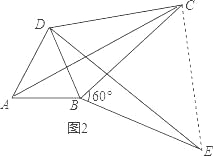
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD、DC,∠DCB=30°.求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
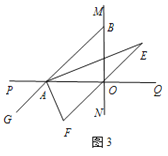
(4)若将图2中△ABC绕顶点B按顺时针方向旋转a度(0°<a<90°),得到△DBE,连接AD、DC,则∠DCB= °,四边形ABCD是勾股四边形.
【答案】(1)矩形;正方形(答案不唯一);(2)详见解析:(3,4)或(4,3);(3)详见解析
【解析】试题分析:(1)根据定义和勾股四边形的性质,有矩形或正方形或直角梯形满足题意;
(2)OM=AB知以格点为顶点的M共两个,分别得出答案;
(3)连接CE,证明△BCE是等边三角形,△DCE是直角三角形,继而可证明四边形ABCD是勾股四边形;
(4)连接CE,证明△DCE是直角三角形,继而可证明四边形ABCD是勾股四边形.
试题解析:(1)学过的特殊四边形中是勾股四边形的两种图形的名称:矩形,正方形;
(2)如图1所示:M(3,4),M(4,3);
(3)如图2,连接CE,由旋转得:△ABC≌△DBE,
∴AC=DE,BC=BE,
∵∠CBE=60,
∴△CBE为等边三角形,
∴BC=CE,∠BCE=60,
∵∠DCB=30,
∴∠DCE=∠DCB+∠BCE=30°+60°=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
∴即四边形ABCD是勾股四边形.
(4)如图3,当∠DCB=![]() ,四边形ABCD是勾股四边形,
,四边形ABCD是勾股四边形,
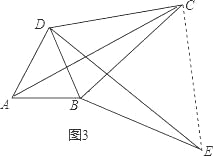
理由:连接CE,
由旋转得:△ABC≌△DBE,
∴AC=DE,BC=BE,
又∵∠CBE=α,
∴∠BCE=∠BEC=90°-![]() ,
,
∴∠DCE=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
∴即四边形ABCD是勾股四边形