题目内容
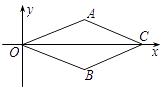
【题目】已知∠MON = 50°,OE 平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D、设∠OAC = x°.
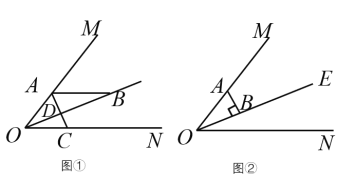
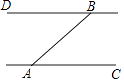
(1)如图①,若AB//ON,
①则∠ABO 的度数是________;
②当∠BAD =∠ABD 时,x=_______;当∠BAD = ∠BDA 时,x=________.
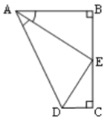
(2)如图②,若AB⊥OE,则是否存在这样的x值,使得 △ABD 中有一个角是另一个角的两倍.存在,直接写出x的值;不存在,说明理由.
【答案】(1)①25°,②105,52.5;(2)存在,x的值为20,110,5,125,35,95.
【解析】
(1)利用角平分线的性质求出∠ABO的度数是关键,利用三角形的内角和定理及其推论计算求解即可.
(2)按点D在线段OB上或OB的延长线上分两大类,再根据△ABD 中有一个角是另一个角的两倍的三种可能性再分类,利用三角形的内角和及其推论分别求解计算即可.
解:(1)①∵∠MON=50°,OE平分∠MON∴∠AOB=∠BON=25°
∵AB∥ON∴∠ABO=25°
②当∠BAD=∠ABD,则∠BAD=25°
∵∠AOB+∠ABO+∠OAB=180°
∴∠AOB+∠ABO+∠OAC+∠BAD=180°
∴∠OAC=180°-∠AOB-∠ABO-∠BAD =180°-25°-25°-25°=105°
当∠BAD=∠BDA,∵∠ABO=25°
∴∠BAD=77.5°
∵∠AOB+∠ABO+∠OAB=180°
∴∠OAB=180°-∠ABO-∠AOB=180°-25°-25°=130°
∴∠OAC=∠OAB-∠BAD=130°-77.5°=52.5°
故答案为:①25°;②105,52.5;
(2)存在,推导如下
当点D在线段OB上时,如图③所示:
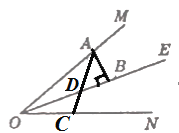
图③
i)当∠ABD=2∠DAB=90°时,则∠ADB=∠DAB=45°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=45°-25°=20°,
ii)当∠ADB=2∠DAB时,∵∠ABD=90°,∴∠ADB=60°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=60°-25°=35°,
iii) 当∠DAB=2∠ADB时, ∵∠ABD=90°,∴∠ADB=30°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=30°-25°=5°.
当点D在线段OB延长线上时,如图③所示:

图③
i)当∠ABD=2∠DAB=90°时,则∠ADB=∠DAB=45°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-45°=110°;
ii)当∠ADB=2∠DAB时,∵∠ABD=90°,∴∠ADB=60°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-60°=95°;
iii) 当∠DAB=2∠ADB时, ∵∠ABD=90°,∴∠ADB=30°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-30°=125°;
综上所述,存在这样的∠OAC,使得 △ABD 中有一个角是另一个角的两倍,其值x
为20,110,5,125,35,95.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案