Question

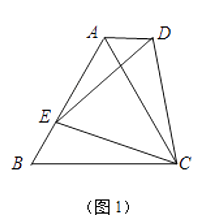
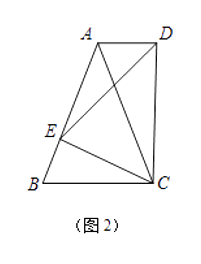
【题目】分如图，在ABCD中，点E、F分别是AD、BC的中点，分别连接BE、DF、BD．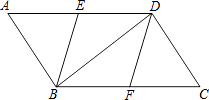

（1）求证：△AEB≌△CFD；
（2）若四边形EBFD是菱形，求∠ABD的度数．

Answer 1

【答案】
（1）证明：∵四边形ABCD是平行四边形，

∴∠A=∠C，AD=BC，AB=CD．

∵点E、F分别是AD、BC的中点，

∴AE= AD，FC= BC．

∴AE=CF．

在△AEB与△CFD中，

，

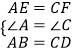∴△AEB≌△CFD（SAS）

（2）解：∵四边形EBFD是菱形，

∴BE=DE．

∴∠EBD=∠EDB．

∵AE=DE，

∴BE=AE．

∴∠A=∠ABE．

∵∠EBD+∠EDB+∠A+∠ABE=180°，

∴∠ABD=∠ABE+∠EBD= ×180°=90°

【解析】（1）利用平行四边形的性质得到对边相等，对角相等，结合已知的“中点”条件，推出△AEB≌△CFD；（2）利用菱形的性质，邻边相等，再结合中点条件，得出AE=DE=BE，利用”一边上的中线等于这边的一半的三角形是直角三角形“得出∠ABD=90°.
【考点精析】通过灵活运用平行四边形的性质，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分即可以解答此题．