题目内容
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点B,与y轴交于点C,抛物线
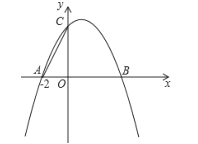
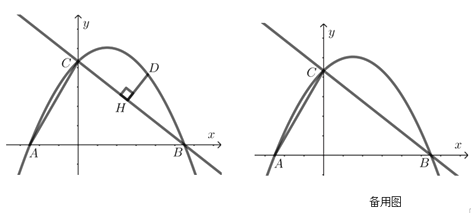
与x轴交于点B,与y轴交于点C,抛物线![]() 经过点B和点C,且与x轴交于另一点A,连接AC,点D在BC上方的抛物线上,设点D的横坐标为m,过点D作DH⊥BC于点H.
经过点B和点C,且与x轴交于另一点A,连接AC,点D在BC上方的抛物线上,设点D的横坐标为m,过点D作DH⊥BC于点H.
(1)求抛物线的函数表达式;
(2)线段DH的长为 (用含m的代数式表示);
(3)点M为线段AC上一点,连接OM绕点O顺时针旋转60°得线段ON,连接CN,当CN=![]() ,m=6时,请直接写出此时线段DM的长.
,m=6时,请直接写出此时线段DM的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)利用待定系数法即可求得解析式;
(2)利用勾股定理列方程计算即可得出;
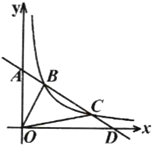
(3)作∠NPO=60°(点P在x轴上),作NQ⊥x轴,交x轴于点Q,
作NH⊥y轴交y轴于点H,作MG⊥x轴交x轴于点G,交DS于点T,DS⊥x轴于点S,
做出辅助线后根据条件讨论即可.
(1)根据![]() 可得B(11,0),C(0,
可得B(11,0),C(0,![]() ),
),
将B,C两点代入![]() ,
,
得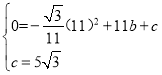 ,解得
,解得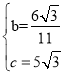 ,
,
∴解析式为:![]() ;
;
(2)由题意可得B(11,0),C(0,![]() ),
),
∴OB=11,OC=![]() ,
,
∵D点的横坐标为m,
∴D点的坐标可表示为(m,![]() )
)
∴|BC|=![]() ,
,
|DC|=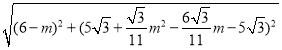 ,
,
|BD|=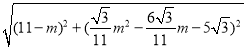 ,
,
设CH=x,
∴|DC|2-x2=|BD|2-(14-x)2
解得x=![]() ,
,
|DH|=![]() ;
;
(3))如图,作∠NPO=60°(点P在x轴上),作NQ⊥x轴,交x轴于点Q,
作NH⊥y轴交y轴于点H,作MG⊥x轴交x轴于点G,交DS于点T,DS⊥x轴于点S,

∵抛物线![]() 交x轴于点A,B,
交x轴于点A,B,
∴令![]()
解得x1=11,x2=-5,
即A(-5,0),OA=5,
∵tan=![]() ,
,
∴∠CAO=60°,∠ACO=30°,
∵∠MON=60°,∠CAO=120°,
∴∠MOA+∠NOP=120°,∠MOA+∠AMO=120°,
∴∠NOP=∠AMO,
在△MOA和△ONP中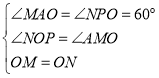 ,
,
∴△MOA≌△ONP(AAS),
∴NP=OA=5,
在Rt△NQP中,QP=NP·cos60°=![]() ,NQ=NP·sin60°=
,NQ=NP·sin60°=![]() ,
,
在四边形NHOQ中,∠NQO=∠QOP=∠OQN=90°,
∴∠HNQ=90°,
∴四边形NHOQ是矩形,
∴OH=NQ=![]() ,CH=OC-OH=
,CH=OC-OH=![]() -
-![]() =
=![]() ,
,
在Rt△CHN中,HN=![]() ,
,
在Rt△HNO中,ON=![]() ,
,
∴OM=ON=![]() ,
,
设MG=a,则GC=![]() =
=![]() ,OG=
,OG=![]() -
-![]() ,
,
在Rt△MOG中,DM2=MG2+OG2,
即212=a2+(![]() -
-![]() )2,整理得:(a-3)(2a-9)=0,
)2,整理得:(a-3)(2a-9)=0,
解得a1=3,a2=![]() ,
,
当m=6时,D(6,![]() ),
),
①a1=3时,MT=3+6=9,TS=OG=![]() ,DT=
,DT=![]() -
-![]() =
=![]() ,
,
在Rt△DMT中,DM=![]() ,
,
②a2=![]() 时,MT=
时,MT=![]() +6=
+6=![]() ,TS=OG=
,TS=OG=![]() ,DT=
,DT=![]() -
-![]() =
=![]() ,
,
在Rt△MDT中,DM=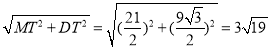 ,
,
综上DM的值为![]() 或
或![]() .
.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案