题目内容
【题目】若一条直线把一个平面图形分成面积相等的两部分,那么这条直线叫做该平面图形的“和谐线”,其“和谐线”被该平面图形截得的线段叫做该平面图形的“和谐线段”(例如圆的直径就是圆的“和谐线段”)
问题探究:
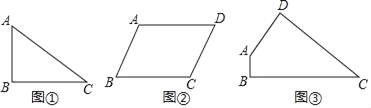
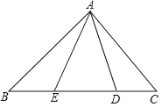
(1)如图①,已知△ABC中,AB=6,BC=8,∠B=90°,请写出△ABC的两条“和谐线段”的长.
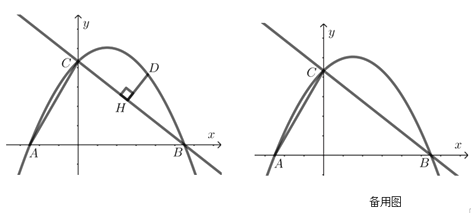
(2)如图②,平行四边形ABCD中,AB=6,BC=8,∠B=60°,请直接写出该平行四边形ABCD的“和谐线段”长的最大值和最小值;
问题解决
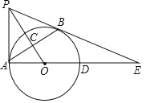
(3)如图③,四边形ABCD是某市规划中的商业区示意图,其中AB=2,CD=10,∠A=135°,∠B=90°,tanC=![]() ,现计划在商业区内修一条笔直的单行道MN(小道的宽度不计),入口M在BC上,出口N在CD上,使得MN为四边形ABCD“和谐线段”,在道路一侧△MNC区域规划为公园,为了美观要求△MNC是以CM为腰的等腰三角形,请通过计算说明设计师的想法能否实现?若可以,请确定点M的位置(即求CM的长).
,现计划在商业区内修一条笔直的单行道MN(小道的宽度不计),入口M在BC上,出口N在CD上,使得MN为四边形ABCD“和谐线段”,在道路一侧△MNC区域规划为公园,为了美观要求△MNC是以CM为腰的等腰三角形,请通过计算说明设计师的想法能否实现?若可以,请确定点M的位置(即求CM的长).
【答案】(1)BD=5,AE=2![]() ,CF=
,CF=![]() ;(2)最小值为3
;(2)最小值为3![]() ,最大值为2
,最大值为2![]() ;(3)可以,CM的值为
;(3)可以,CM的值为![]()
【解析】
(1)作△ABC的中线AE,BD,CF.线段AE,BD,CF都是△ABC的和谐线段.
(2)作AE⊥BC于E,CF⊥AB于F,连接AC,BD交于点O.经过点O的直线都是平行四边形ABCD的“和谐线”.求出平行四边形对边之间的距离,对角线的从即可判断.
(3)构造直角三角形,求出四边形ABCD的面积,分两种情形分别求解即可.
(1)作△ABC的中线AE,BD,CF.线段AE,BD,CF都是△ABC的和谐线段.

在Rt△ABC中,∵∠ABC=90°,AB=6,BC=8,
∴AC=![]() =10,
=10,
∴BD=![]() AC=5,AE=
AC=5,AE=![]() =2
=2![]() ,CF=
,CF=![]() =
=![]() .
.
(2)作AE⊥BC于E,CF⊥AB于F,连接AC,BD交于点O.经过点O的中线都是平行四边形ABCD的“和谐线”.
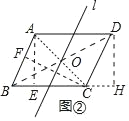
在Rt△ABE中,∵∠AEB=90°,AB=6,∠ABE=60°,
∴AE=ABsin60°=3![]() ,
,
同法可求:CF=4![]() ,
,
∴平行四边形ABCD的“和谐线段”长的最小值为3![]() ,
,
作DH⊥BC交BC的延长线于H.易知CH=BE=3,
在Rt△BDH中,BD=![]() =
=![]() =2
=2![]() ,
,
在Rt△ACE中,AC=![]() =
=![]() =2
=2![]() ,
,
∴平行四边形ABCD的“和谐线段”长的最大值为2![]() .
.
(3)如图③﹣1中,作DE⊥BC于E,AF⊥DE于F.
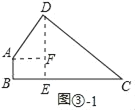
在Rt△CDE中,∵CD=10,tanC=![]() ,
,
∴DE=6,EC=8,
∵四边形ABEF是矩形,
∴AB=EF=2,
∴DF=4,
∵∠DAB=135°,∠BAF=90°,
∴∠DAF=45°,
∴AF=BE=DF=4,
∴BC=4+8=12,
∴S四边形ABCD=![]() (2+6)×4+
(2+6)×4+![]() ×6×8=40,
×6×8=40,
如图③﹣2中,当CM=CN时,设CM=CN=x.
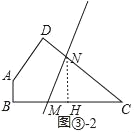
∵tanC=![]() =
=![]() ,
,
∴NH=![]() x,
x,
∵S△MNC=20,
∴![]()
![]() xx=20,
xx=20,
∴x=![]() 或﹣
或﹣![]() (舍弃).
(舍弃).
如图③﹣3中,当CM=MN时,设CM=MN=x.作MH⊥CN于H.

∵MC=MN,MH⊥CN,
∴CH=HN,
∵tanC=![]() =
=![]() ,
,
∴MH=![]() x,CH=
x,CH=![]() x,
x,
∴CN=![]() x,
x,
∴![]()
![]() x
x![]() x=20,
x=20,
∴x=![]() 或(﹣
或(﹣![]() )
)
此时CN>10,不符合题意舍弃,
综上所述,满足条件的CM的值为![]() .
.