题目内容
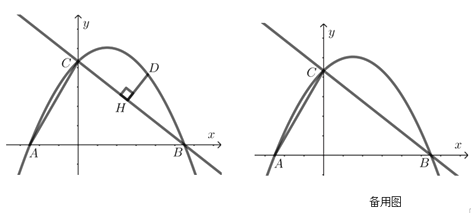
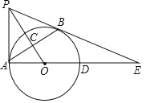
【题目】如图所示,![]() 、
、![]() 、
、![]() 在第二象限,横坐标分别是-4、-2、-1,双曲线
在第二象限,横坐标分别是-4、-2、-1,双曲线![]() 过
过![]() 、
、![]() 、
、![]() 三点,且
三点,且![]() .
.
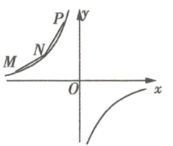
(1)求双曲线的解析式;
(2)过![]() 点的直线
点的直线![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,且
,且![]() ,且交
,且交![]() 于另一点
于另一点![]() ,求
,求![]() 点坐标;
点坐标;
(3)以![]() 为边(顺时针方向)作正方形
为边(顺时针方向)作正方形![]() ,平移正方形使
,平移正方形使![]() 落在
落在![]() 轴上,点
轴上,点![]() 、
、![]() 对应的点
对应的点![]() 、
、![]() 正好落在反比例函数
正好落在反比例函数![]() 上,求
上,求![]() 对应点
对应点![]() 的坐标.
的坐标.
【答案】(1) ![]() ;(2)点
;(2)点![]() ;(3)
;(3) ![]()
【解析】
(1)由题可得![]() ,根据
,根据![]() 利用勾股定理列式求出k;
利用勾股定理列式求出k;
(2)由(1)得![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,得到
,得到![]() ,求出B(0,1),求出直线PB的解析式
,求出B(0,1),求出直线PB的解析式![]() ,与反比例函数联立求交点即可得到点Q的坐标;
,与反比例函数联立求交点即可得到点Q的坐标;
(3)过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,求出
,求出![]() ,由平移后
,由平移后![]() 在
在![]() 轴上得到
轴上得到![]() 纵坐标为0,推出
纵坐标为0,推出![]() 纵坐标分别为2和1,得到
纵坐标分别为2和1,得到![]() ,列式得
,列式得![]() ,即可求出b,得到平移的规律,求出点F的坐标.
,即可求出b,得到平移的规律,求出点F的坐标.
(1)由题可得![]()
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)由(1)得![]()
过![]() 作
作![]() 轴于
轴于![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
设![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,
,
![]() .
.
解 可得另一交点
可得另一交点![]() ;
;
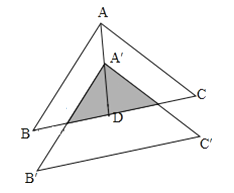
(3)如图所示,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
由![]() 是正方形可得
是正方形可得![]() .
.
![]() .
.
![]() .
.
∵平移后![]() 在
在![]() 轴上,
轴上,
∴![]() 纵坐标为0.
纵坐标为0.
∴![]() 纵坐标分别为2和1.
纵坐标分别为2和1.
∵![]() 都在
都在![]() 上,
上,
![]()
![]() .
.
![]() .
.
![]() .
.
可知![]() 向左平移2格,向下平移2格.
向左平移2格,向下平移2格.
![]() .
.


练习册系列答案
相关题目