题目内容
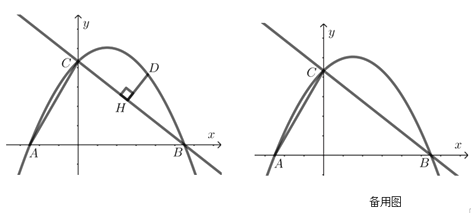
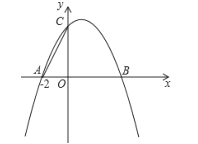
【题目】如图，已知抛物线
与
轴交于
、
两点，与
轴交于
点，其对称轴为直线
．
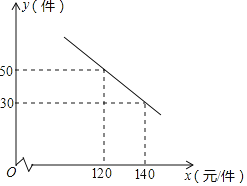
（1）直接写出抛物线的解析式；
（2）把线段
沿轴向右平移，设平移后
、的对应点分别为
、
，当落在抛物线上时，求、的坐标；
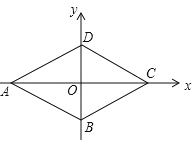
（3）除（2）中的平行四边形
外，在轴和抛物线上是否还分别存在点
、
，使得以、、、为顶点的四边形为平行四边形？若存在，求出、的坐标；若不存在，请说明理由．
【答案】（1）
；（2）
，
；（3）
，
；
，
；
，
【解析】
（1）先求得B点的坐标，然后根据待定系数法交点抛物线的解析式；
（2）根据平移性质及抛物线的对称性，求出A′、C′的坐标；
（3）以A、C、E、F为顶点的四边形为平行四边形，可能存在3种满足条件的情形，需要分类讨论，避免漏解．
解：（1）∵A（-2，0），对称轴为直线x=1．
∴B（4，0），
把A（-2，0），B（4，0）代入抛物线的表达式为：
，
解得：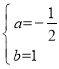
，
∴抛物线的解析式为：y=-
x2+x+4；
（2）由抛物线y=-x2+x+4可知C（0，4），
∵抛物线的对称轴为直线x=1，根据对称性，
∴C′（2，4），
∴A′（0，0）．
（3）存在．
设F（x，-x2+x+4）．
以A、C、E、F为顶点的四边形为平行四边形，
①若AC为平行四边形的边，如答图1-1所示，则EF∥AC且EF=AC．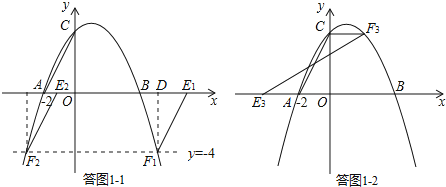
过点F1作F1D⊥x轴于点D，则易证Rt△AOC≌Rt△E1DF1，
∴DE1=2，DF1=4．
∴-x2+x+4=-4，
解得：x1=1+
，x2=1-．
∴F1（1+，-4），F2（1-，-4）；
∴E1（3+，0），E2（3-，0）．
②若AC为平行四边形的对角线，如答图1-2所示．
∵点E3在x轴上，∴CF3∥x轴，
∴点C为点F关于x=1的对称点，
∴F3（2，4），CF3=2．
∴AE3=2，
∴E3（-4，0），
综上所述，存在点E、F，使得以A、C、E、F为顶点的四边形为平行四边形；
点E、F的坐标为：，；，；，
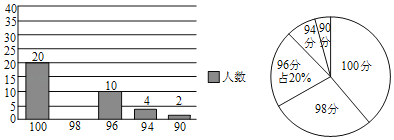
【题目】
某校为了解七、八年级学生对“新冠”传播与防治知识的掌握情况，从七、八年级各随机抽取50名学生进行测试，并对成绩（百分制）进行整理和分析．部分信息如下：
a．七年级成绩频数分布直方图：
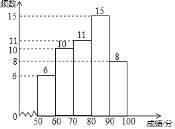
b．七年级成绩在70
m
80这一组的是：
70，72，72，75，76，76，77，77，78，79，79
c．七、八年级成绩的平均数、中位数如下：
年级 | 平均数 | 中位数 |
七 | 76.9 | a |
八 | 79.2 | 79.5 |
根据以上信息，回答下列问题：
（1）在这次测试中，七年级在70分以上的有 人，表格中a的值为 ；
（2）在这次测试中，七年级学生甲与八年级学生乙的成绩都是79分，请判断两位学生在各自年级的排名谁更靠前；
（3）该校七年级学生有500人，假设全部参加此次测试，请你估计七年级成绩超过平均数76.9分的人数．
