题目内容
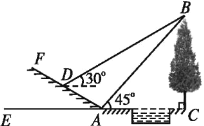
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是45°,若坡角∠FAE=30°,求大树的高度(结果保留根号).
【答案】大树的高度为(9+3![]() )米
)米
【解析】
根据矩形性质得出![]() ,再利用锐角三角函数的性质求出问题即可.
,再利用锐角三角函数的性质求出问题即可.
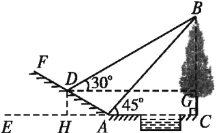
解:如图,过点D作DG⊥BC于G,DH⊥CE于H,
则四边形DHCG为矩形.
故DG=CH,CG=DH,在![]() 中,∵∠DAH=30°,AD=6米,
中,∵∠DAH=30°,AD=6米,
∴DH=3米,AH=3![]() 米,
米,
∴CG=3米,
设BC![]() 米,
米,
在![]() 中,∠BAC=45°,∴AC
中,∠BAC=45°,∴AC![]() 米,
米,
∴DG=(3![]() +
+![]() )米,BG=(
)米,BG=(![]() )米,
)米,
在![]() 中,
中,
∵BG=DG·tan 30°,
∴![]() (3
(3![]()
![]() )×
)×![]() ,
,
解得:![]() 9+3
9+3![]() ,
,
∴BC=(9+3![]() )米.
)米.
答:大树的高度为(9+3![]() )米.
)米.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目