Question

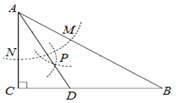
【题目】如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AF=CE，DF=BE，且DF∥BE，过点C作CG⊥AB交AB延长线与点G．

（1）求证：四边形ABCD是平行四边形；

（2）若tan∠CAB=，∠CBG=45°，BC=，则ABCD的面积是　　　　．

Answer 1

【答案】（1）证明见解析；（2）24．

【解析】

（1）先根据已知条件证明△DFA≌△BEC，根据全等三角形的性质可得AD=CB，∠DAF=∠BCE，然后可推出AD∥CB，即可证明四边形ABCD是平行四边形；

（2）根据已知可得△BCG是等腰直角三角形，从而求出BG=CG=4，解直角三角形得AG=10，AB=6，即可求出平行四边形的面积．

（1）证明：∵DF∥BE，

∴∠DFA=∠BEC

∵AE=CF，

∴AE+EF=CF+EF，

∴AF=CE，

在△DFA和△BEC中，

∴△DFA≌△BEC，

∴AD=CB，∠DAF=∠BCE，

∴AD∥CB，

∴四边形ABCD是平行四边形；

（2）∵∠CBG=45°

∴△BCG是等腰直角三角形，

∵BC=，

∴BG=CG=4，

∵tan∠CAB=，

∴AG=10，AB=6，

∴平行四边形ABCD的面积=4×6=24．