题目内容
【题目】已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B,C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.
初步感知:
(1)如图1,当点D在边BC上时,①求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
(3)如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.
【答案】
(1)
①证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵∠DAF=60°,
∴∠BAC=∠DAF,
∴∠BAD=∠CAF,
∵四边形ADEF是菱形,
∴AD=AF,
在△ABD和△ACF中, 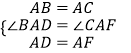 ,
,
∴△ABD≌△ACF(SAS),
∴∠ADB=∠AFC,
②解:∠AFC=∠ACB+∠DAC成立.理由如下:
∵△ABD≌△ACF,
∴∠ADB=∠AFC,
∵∠ADB=∠ACB+∠DAC,
∴∠AFC=∠ACB+∠DAC
问题探究:
(2)
解:∠AFC=∠ACB+∠DAC不成立.
∠AFC、∠ACB、∠DAC之间的等量关系是∠AFC=∠ACB﹣∠DAC.理由如下:
∵△ABC为等边三角形,
∴AB=AC,
∠BAC=60°,
∵∠BAC=∠DAF,
∴∠BAD=∠CAF,
∵四边形ADEF是菱形,
∴AD=AF.
在△ABD和△ACF中, 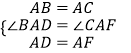 ,
,
∴△ABD≌△ACF(SAS).
∴∠ADB=∠AFC.
又∵∠ACB=∠ADC+∠DAC,
∴∠AFC=∠ACB﹣∠DAC
类比分析:
(3)
解:补全图形如图所示:
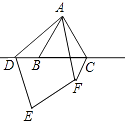
∠AFC、∠ACB、∠DAC之间的等量关系是:∠AFC+∠DAC+∠ACB=180°;理由如下:
同(2)得:△ABD≌△ACF,
∴∠ADC=∠AFC,
∵∠ADC+∠ACB+∠DAC=180°,
∴∠AFC+∠DAC+∠ACB=180°.
【解析】(1)①由AB=AC,AD=AF,∠BAD=∠CAF,按照SAS判断两三角形全等得出∠ADB=∠AFC;②由全等三角形的性质和三角形的外角性质即可得出结论;(2)此题应先判断得出正确的等量关系,然后再根据△ABD≌△ACF即可证明;(3)补全图形后由图形,由全等三角形的性质和三角形内角和定理即可得出∠AFC、∠ACB、∠DAC之间存在的等量关系.