题目内容
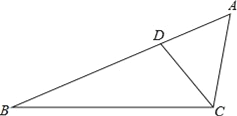
【题目】如图1,四边形ABCD是正方形,点E是AB边的中点,以AE为边作正方形AEFG,连接DE,BG.
(1)发现
①线段DE、BG之间的数量关系是;
②直线DE、BG之间的位置关系是 .
(2)探究
如图2,将正方形AEFG绕点A逆时针旋转,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)应用
如图3,将正方形AEFG绕点A逆时针旋转一周,记直线DE与BG的交点为P,若AB=4,请直接写出点P到CD所在直线距离的最大值和最小值.
【答案】
(1)DE=BG;DE⊥BG
(2)
解:(1)中的结论仍然成立,理由是:
①如图3,∵四边形AEFG和四边形ABCD是正方形,
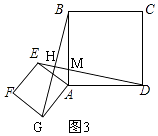
∴AE=AG,AD=AB,∠EAG=∠DAB=90°,
∴∠EAD=∠GAB=90°+∠EAB,
在△EAD和△GAB中,
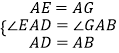 ,
,
∴△EAD≌△GAB(SAS),
∴ED=GB;
②ED⊥GB,
理由是:∵△EAD≌△GAB,
∴∠GBA=∠EDA,
∵∠AMD+∠ADM=90°,∠BMH=∠AMD,
∴∠BMH+∠GBA=90°,
∴∠DHB=180°﹣90°=90°,
∴ED⊥GB;
(3)
解:应用
将正方形AEFG绕点A逆时针旋转一周,即点E和G在以A为圆心,以2为半径的圆上,
过P作PH⊥CD于H,
①当P与F重合时,此时PH最小,如图4,

在Rt△AED中,AD=4,AE=2,
∴∠ADE=30°,DE= ![]() =2
=2 ![]() ,
,
∴DF=DE﹣EF=2 ![]() ﹣2,
﹣2,
∵AD⊥CD,PH⊥CD,
∴AD∥PH,
∴∠DPH=∠ADE=30°,
cos30°= ![]() =
= ![]() ,
,
∴PH= ![]() (2
(2 ![]() ﹣2)=3﹣
﹣2)=3﹣ ![]() ;
;
②∵DE⊥BG,∠BAD=90°,
∴以BD的中点O为圆心,以BD为直径作圆,P、A在圆上,
当P在 ![]() 的中点时,如图5,此时PH的值最大,
的中点时,如图5,此时PH的值最大,
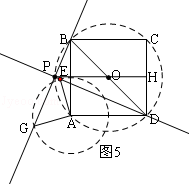
∵AB=AD=4,
由勾股定理得:BD=4 ![]() ,
,
则半径OB=OP=2 ![]()
∴PH=2+2 ![]() .
.
综上所述,点P到CD所在直线距离的最大值是2+2 ![]() ,最小值是3﹣
,最小值是3﹣ ![]() .
.
【解析】解:(1)发现①线段DE、BG之间的数量关系是:DE=BG,
理由是:如图1,∵四边形ABCD是正方形,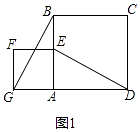
∴AB=AD,∠BDA=90°,
∴∠BAG=∠BAD=90°,
∵四边形AEFG是正方形,
∴AE=AG,
∴△AED≌△AGB,
∴DE=BG;②直线DE、BG之间的位置关系是:DE⊥BG,
理由是:如图2,延长DE交BG于Q,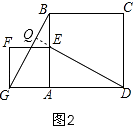
由△AED≌△AGB得:∠ABG=∠ADE,
∵∠AED+∠ADE=90°,∠AED=∠BEQ,
∴∠BEQ+∠ABG=90°,
∴∠BQE=90°,
∴DE⊥BG;
所以答案是:①DE=BG;②DE⊥BG;
【考点精析】关于本题考查的图形的旋转,需要了解每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能得出正确答案.