题目内容
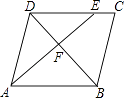
【题目】如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上,折痕的一端E点在边BC上,BE=10.则折痕的长为 . 
【答案】5 ![]() 或4
或4 ![]()
【解析】解:(1)如图(1)所示:过点E作EH⊥AD于点H,则AH=BE=10,FE=AB=8, 
∵△GFE由△BFE翻折而成,
∴GE=BE=10,
在Rt△EGH中,
∵GH= ![]() =
= ![]() =6,
=6,
∴AG=AH﹣GH=10﹣6=4,
设AF=x,则BF=GF=8﹣x,
在Rt△AGF中,
∵AG2+AF2=GF2 , 即42+x2=(8﹣x)2 , 解得x=3,
∴BF=8﹣3=5,
在Rt△BEF中,
EF= ![]() =
= ![]() =5
=5 ![]() .(2)连接BF、BG与折痕EF交于O,如图(2)
.(2)连接BF、BG与折痕EF交于O,如图(2)
由于折叠,
∴BG⊥EF,BO=OG,BE=GE,
四边形ABCD为长方形,
∴AD∥BC
∴∠FGO=∠OBE,
∴△BOE≌△GOF(ASA),
∴OF=OE,又OB=OG,BG⊥EF
∴四边形BEGF是菱形,
∴BF=BE=10;
Rt△ABF中,AF2+AB2=BF2 ,
AF2=102﹣82 ,
解得AF=6.
则有BL=6,
LE=10﹣6=4,
在Rt△FLE中,由勾股定理得:
FE= ![]() =4
=4 ![]() .
.
所以答案是:5 ![]() 或4
或4 ![]() .
.
【考点精析】掌握翻折变换(折叠问题)是解答本题的根本,需要知道折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

 小题狂做系列答案
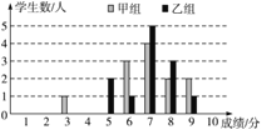
小题狂做系列答案【题目】(8分)一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分为优秀.这次测验中甲、乙两组学生成绩分布的条形统计图如图.
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.