题目内容
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为 ![]() .
. 
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
【答案】
(1)解:设绿球的个数为x.由题意,得 ![]() =
= ![]()
解得x=1,经检验x=1是所列方程的根,所以绿球有1个
(2)解:根据题意,画树状图:
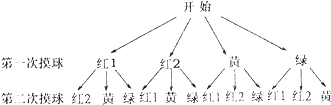
由图知共有12种等可能的结果,
即(红1,红2),(红1,黄),(红1,绿),(红2,红1),(红2,黄),(红2,绿),(黄,红1),(黄,红2),(黄,绿),(绿,红1),(绿,红2),(绿,黄),其中两次都摸到红球的结果有两种(红,红),(红,红).
∴P(两次都摸到红球)= ![]() =
= ![]() ;
;
或根据题意,画表格:
第1次 第2次 | 红1 | 红2 | 黄 | 绿 |
红1 | (红2,红1) | (黄,红1) | (绿,红1) | |
红2 | (红1,红2) | (黄,红2) | (绿,红2) | |
黄 | (红1,黄) | (红2,黄) | (绿,黄) | |
绿 | (红1,绿) | (红2,绿) | (黄,绿) |
由表格知共有12种等可能的结果,其中两次都摸到红球的结果有两种,
∴P(两次都摸到红球)= ![]() =
= ![]()
【解析】(1)此题的求解方法是:借助于方程求解;(2)此题需要两步完成,所以采用树状图或者列表法都比较简单.

 轻巧夺冠周测月考直通中考系列答案
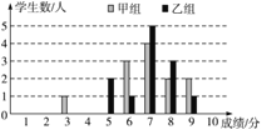
轻巧夺冠周测月考直通中考系列答案【题目】(8分)一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分为优秀.这次测验中甲、乙两组学生成绩分布的条形统计图如图.
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.