题目内容
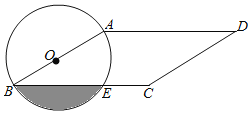
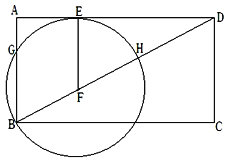
【题目】如图,已知,矩形ABCD中,F是对角线BD上一点,以F为圆心,FB为半径作圆与边AD相切于E,边AB与圆F交于另一点G.
(1)若四边形BGEF是菱形,求证:∠EFD=60o;
(2)若AB=15,AD=36,求AE的长;
(3)若BD与圆F交于另一点H,求证:![]() .
.
【答案】(1)60°;(2)AE=10;(3)详见解析
【解析】
(1)根据菱形的性质得到△GEF和△BGF都是等边三角形,根据等边三角形的性质计算,得到答案;
(2)根据勾股定理求出BD,由△DEF∽△DAB,根据相似三角形的性质列出比例式,计算即可;
(3)连BE,EH,分别证明△AGE∽△EHB和△DEH∽△DBE,根据相似三角形的性质证明结论.
解:(1)在菱形BGEF中,BG=GE=EF=FB
∵FG=FE=FB
∴△GEF和△BGF都是等边三角形,
∴∠EFD=180°-60°-60°=60°;
(2)∵AB=15,AD=36,
∴DB=39
∵△DEF∽△DAB;设EF=BF=r,设AE=x,
∴![]()
解得:![]()
![]()
∴AE=10
(3)连BE,EH,
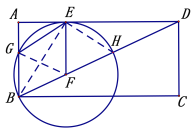
∵BH为直径,
∴∠BEH=90°,
∴∠BEH=∠EAG,
∵四边形GBHE是圆内接四边形,
∴∠BHE=∠EGA,
∴△AGE∽△EHB,
∴![]()
∵AD是圆的切线,
∴∠DEH=∠DBE,又∠EDH=∠BDE,
∴△DEH∽△DBE,
∴![]() ,
,
∴![]() 即
即![]() .
.

练习册系列答案
相关题目