题目内容
【题目】 阅读并补充下面推理过程：（1）
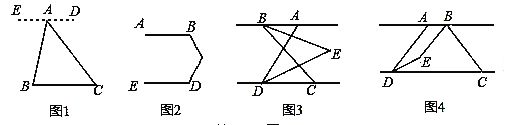
如图1，已知点A是BC外一点，连接AB，AC．
求∠BAC+∠B+∠C的度数．
解：过点A作ED∥BC，所以∠B= ，∠C= ．
又因为∠EAB+∠BAC+∠DAC=180°．
所以∠B+∠BAC+∠C=180°．
方法运用：（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数．
深化拓展：（3）已知AB∥CD，点C在点D的右侧，∠ADC=70°，BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间．
．如图3，点B在点A的左侧，若∠ABC=60°，则∠BED的度数为 °．
Ⅱ．如图4，点B在点A的右侧，且AB＜CD，AD＜BC．若∠ABC=n°，则∠BED的度数为 °．（用含n的代数式表示）
【答案】（1）∠B=∠EAB，∠C=∠DAC
（2）∠B+∠BCD+∠D的度数为3600；
（3）．∠BED的度数为65；Ⅱ．∠BED的度数为
°
【解析】试题分析：（1）根据平行线的性质即可得到结论；
（2）过C作CF∥AB根据平行线的性质得到∠D=∠FCD，∠B=∠BCF，然后根据已知条件即可得到结论；
（3）A.过点E作EF∥AB，然后根据两直线平行内错角相等，即可求∠BED的度数；
B.∠BED的度数改变．过点E作EF∥AB，先由角平分线的定义可得：∠ABE=
∠ABC=
n°，∠CDE=
∠ADC=35°，然后根据两直线平行内错角相等及同旁内角互补可得：∠BEF=180°-∠ABE=180°-
n°，∠CDE=∠DEF=35°，进而可求∠BED=∠BEF+∠DEF=180°-
n°+35°=215°-
n°．
试题解析：（1）∵ED∥BC，∴∠B=∠EAD，∠C=∠DAE，
（2）过C作CF∥AB，
∵AB∥DE，
∴CF∥DE，
∴∠D=∠FCD，
∵CF∥AB，
∴∠B=∠BCF，
∵∠BCF+∠BCD+∠DCF=360°，
∴∠B+∠BCD+∠D=360°，
（3）A、如图2，过点E作EF∥AB，
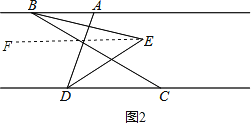
∵AB∥CD，
∴AB∥CD∥EF，
∴∠ABE=∠BEF，∠CDE=∠DEF，
∵BE平分∠ABC，DE平分∠ADC，∠ABC=60°，∠ADC=70°，
∴∠ABE=
∠ABC=30°，∠CDE=
∠ADC=35°，
∴∠BED=∠BEF+∠DEF=30°+35°=65°；
B、如图3，过点E作EF∥AB，
∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=70°
∴∠ABE=
∠ABC=
n°，∠CDE=
∠ADC=35°
∵AB∥CD，
∴AB∥CD∥EF，
∴∠BEF=180°-∠ABE=180°-
n°，∠CDE=∠DEF=35°，
∴∠BED=∠BEF+∠DEF=180°-
n°+35°=215°-
n°．
