题目内容
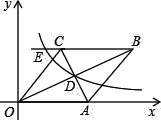
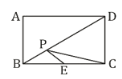
【题目】如图，点
为矩形
的对角线
上一动点，
，
，点
为
边的中点，则
周长的最小值是_________．
【答案】
【解析】
先确定出点P的位置,再求出∠CBD=30°，进而判断出△BCC是等边三角形,即可得出结论．
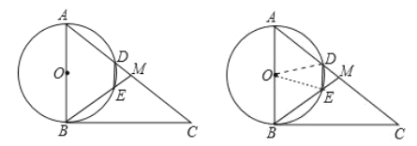
解：如图,作点C关于BD的对称点C,连接EC交BD于点P,连接PC,
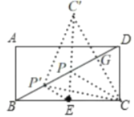
∵点C与点C是关于BD的对称点,
∴CP=CP,
∴CP+PE=CP+PE=CE,
在BD上任取异于点P的P，连接PE,PC,CP,
CP+PE=PC+PE>CE,
∴点P就是所要求作的点，EC的长度PE + PC的最小值,
∵四边形ABCD是矩形,
∴∠BCD=90°
∵DC=AB=2, 
∵tan∠CBD=
∴∠ CBD= 30°,
∴点C和点C关于BD对称，设CC交BD于G,
∴ BD是CC的垂直平分线，连接BC
∴∠CBD=∠CBD=30°, BC=BC,
∴∠ CBC= 60°,
∴△BCC是等边三角形,
∵点E是BC的中点，∴CE⊥BC,
∴CE=
∴PC+PE=3, ∵E是BC的中点，∴CE=
∴
周长的最小值是:PC+PE+CE=3+
故答案为：3+
练习册系列答案
相关题目
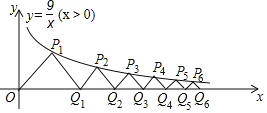
【题目】一辆汽车油箱中有汽油
.如果不再加油，那么油箱中的油量
（单位：
）随行驶路程
（单位：
）的增加而减少.已知该汽车平均耗油量为
.
（Ⅰ）计算并填写下表：
| 10 | 100 | 300 | … |
| … |
（Ⅱ）写出表示与的函数关系式，并指出自变量的取值范围；
（Ⅲ）若
，
两地的路程约有
，当油箱中油量少于
时，汽车会自动报警，则这辆汽车在由地到
地，再由地返回地的往返途中，汽车是否会报警？请说明理由.
