题目内容
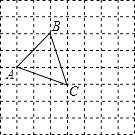
【题目】如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形:
①△ABC≌△DBE;②△ACB≌△ABD;
③△CBE≌△BED;④△ACE≌△ADE.
这些三角形真的全等吗?简要说明理由.

【答案】①△ABC≌△DBE,②△ACB与△ABD不全等,③△CBE与△BED不全等,④△ACE与△ADE不全等,理由见解析
【解析】
根据△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,利用全等三角形的判定定理对4个小题逐个分析即可.
解:①△ABC≌△DBE,BC=BE,∠ABC=∠DBE=90°,AB=BD,符合SAS;
②△ACB与△ABD不全等,因为它们的形状不相同,
△ACB只是直角三角形,△ABD是等腰直角三角形;
③△CBE与△BED不全等,理由同②;
④△ACE与△ADE不全等,它们只有一边一角对应相等.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目