题目内容
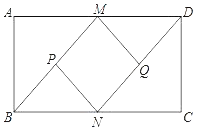
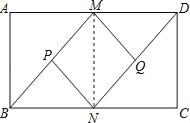
【题目】已知：如图，在矩形ABCD中，M、N分别是AD、BC的中点，P、Q分别是BM、DN的中点．
（1）求证：BM∥DN；
（2）求证：四边形MPNQ是菱形；
（3）矩形ABCD的边长AB与AD满足什么数量关系时四边形MPNQ为正方形，请说明理由．
【答案】（1）详见解析；（2）详见解析；（3）当AB＝
AD时，四边形MPNQ为正方形，理由详见解析.
【解析】
（1）因为M，N分别是AD，BC的中点，由矩形的性质可得DM＝BN，DM∥BN，利用平行四边形的判定和性质可得结论；
（2）由四边形DMBN是平行四边形，求出BM＝DN，BM∥DN，求出三角形MPNQ是平行四边形，根据直角三角形斜边上中线性质求出MQ＝NQ，根据菱形判定推出即可．
（3）根据正方形的性质进行解答即可．
证明：（1）∵四边形ABCD是矩形，
∴AD∥BC，AD＝BC，
∵M、N分别AD、BC的中点，
∴DM＝BN，
∴四边形DMBN是平行四边形；
∴BM∥DN；
（2）∵四边形DMBN是平行四边形，
∴BM＝DN，BM∥DN，
∵P、Q分别BM、DN的中点，
∴MP＝NQ，MP∥NQ，
∴四边形MPNC是平行四边形，
连接MN，
∵四边形ABCD是矩形，
∴AD∥BC，AD＝BC，
∵M、N分别AD、BC的中点，
∴DM＝CN，
∴四边形DMNC是矩形，
∴∠DMN＝∠C＝90°，
∵Q是DN中点，
∴MQ＝NQ，
∴四边形MPNQ是菱形．
（3）当AB＝AD时，四边形MPNQ为正方形，
理由：∵AB＝AD，
∴AB＝AM，
∴矩形ABNM是正方形，
∵P为正方形ABNM对角线BM的中点，
∴∠NPM＝90°，
∵四边形MPNQ是菱形，
∴四边形MPNQ是正方形．
练习册系列答案
相关题目
