题目内容
【题目】在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
【答案】2![]() 或2
或2![]() 或3
或3![]()
【解析】
根据题意中的△ABD为等腰直角三角形,显然应分为三种情况:∠ABD=90°,∠BAD=90°,∠ADB=90°.然后巧妙构造辅助线,出现全等三角形和直角三角形,利用全等三角形的性质和勾股定理进行求解.
∵AC=4,BC=2,![]()
∴AC2+BC2=AB2,
∴△ACB为直角三角形,
∠ACB=90°.
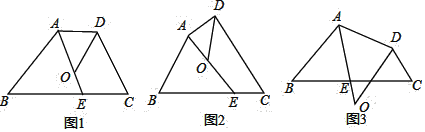
分三种情况:如图(1),过点D作DE⊥CB,垂足为点E.
∵DE⊥CB,
∴∠BED=∠ACB=90°,
∴∠CAB+∠CBA=90°.
∵△ABD为等腰直角三角形,
∴AB=BD,∠ABD=90°,
∴∠CBA+∠DBE=90°,
∴∠CAB=∠EBD.
在△ACB与△BED中,
∵∠ACB=∠BED,∠CAB=∠EBD,AB=BD,
∴△ACB≌△BED(AAS),
∴BE=AC=4,DE=CB=2,
∴CE=6.根据勾股定理得![]()
如图(2),过点D作DE⊥CA,垂足为点E.
∵BC⊥CA,∴∠AED=∠ACB=90°,
∴∠EAD+∠EDA=90°.
∵△ABD为等腰直角三角形,∴AB=AD,∠BAD=90°,
∴∠CAB+∠DAE=90°,
∴∠BAC=∠ADE.在△ACB与△DEA中,
∵∠ACB=∠DEA,∠CAB=∠EDA, AB=DA,
∴△ACB≌△DEA(AAS),
∴DE=AC=4,AE=BC=2,
∴CE=6,根据勾股定理得![]()
如图(3),过点D作DE⊥CB,垂足为点E,过点A作AF⊥DE,垂足为点F.∵∠C=90°,
∴∠CAB+∠CBA=90°.
∵∠DAB+∠DBA=90°,
∴∠EBD+∠DAF=90°.
∵∠EBD+∠BDE=90°,∠DAF+∠ADF=90°,
∴∠DBE=∠ADF.
∵∠BED=∠AFD=90°,DB=AD,
∴△AFD≌△DEB,则ED=AF.
由∠ACB=∠CED=∠AFE=90°,则四边形CEFA是矩形,故CE=AF,EF=AC=4.
设DF=x,则BE=x,故EC=2+x,AF=DE=EF-DF=4-x,则2+x=4-x,解得x=1,
故EC=DE=3,
则![]()