题目内容
【题目】学校的某社团组织了一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a满分10分,题b、题c满分均为15分.竞赛结果,每个学生至少答对了一题,三题全答对的有2人,答对其中两道题的有14人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为27,答对题b的人数与答对题c的人数之和为20,则这个社团的平均成绩是_____分.
【答案】24
【解析】
设答对a题的有x人,答对b题的有y人,答对c题的有z人,根据“答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为27,答对题b的人数与答对题c的人数之和为20”,即可得出关于x、y、z的三元一次方程组,解之即可得出x、y、z的值,由x、y、z的值结合a、b、c三题的分值可求出全社团总得分,由x、y、z的值结合答对两题及答对三题的人数可求出全社团总人数,再利用平均分=总分÷人数,即可求出结论.
解:设答对a题的有x人,答对b题的有y人,答对c题的有z人,
根据题意得: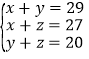 ,
,
解得: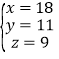 .
.
全社团总得分为18×10+(11+9)×15=480(分),
全社团总人数为18+11+9﹣1×14﹣2×2=20(人),
全社团的平均成绩为480÷20=24(分).
故答案为:24.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目