题目内容
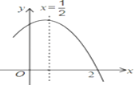
【题目】如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为x=
，且经过点（2，0），有下列说法：①abc>0；②a+b=0；③4a+2b+c ＜0；④若（0，y1），（1，y2）是抛物线上的两点，则y1=y2．上述说法正确的是（ ）
A. ①②④ B. ②④ C. ①③④ D. ①②
【答案】B
【解析】
①根据抛物线开口方向、对称轴位置、抛物线与y轴交点位置求得a、b、c的符号；②根据对称轴求出b=-a；③把x=2代入函数关系式，结合图象判断函数值与0的大小关系；④求出点（0，y1）关于直线x=
的对称点的坐标，根据对称轴即可判断y1和y2的大小．
①∵二次函数的图象开口向下，
∴a＜0，
∵二次函数的图象交y轴的正半轴于一点，
∴c＞0，
∵对称轴是直线x=，
∴-
＝，
∴b=-a＞0，
∴abc＜0．
故①错误；
②∵由①中知b=-a，
∴a+b=0，
故②正确；
③把x=2代入y=ax2+bx+c得：y=4a+2b+c，
∵抛物线经过点（2，0），
∴当x=2时，y=0，即4a+2b+c=0，
故③错误；
④∵（0，y1）关于直线x=的对称点的坐标是（1，y1），
∴y1=y2．
故④正确；
综上所述，正确的结论是：②④．
故选：B．
练习册系列答案
名校课堂系列答案
相关题目
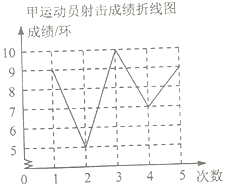
【题目】第16届省运会在我市隆重举行，推动了我市各校体育活动如火如荼的开展，在某校射箭队的一次训练中，甲，乙两名运动员前5箭的平均成绩相同，教练将两人的成绩绘制成如下尚不完整的统计图表.
乙运动员成绩统计表(单位：环)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
8 | 10 | 8 | 6 |
|
(1)甲运动员前5箭射击成绩的众数是 环，中位数是 环；
(2)求乙运动员第5次的成绩；
(3)如果从中选择一个成绩稳定的运动员参加全市中学生比赛，你认为应选谁去？请说明理由.
